


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.2.9. Nosacītā ekstrēma pietiekamie nosacījumi
Augstāk: 1.2. Nosacītais ekstrēms
Iepriekšējais: 1.2.7. Lagranža reizinātāju metodes pamatojums
- 4.
Atrast punktam 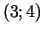 vistuvāko punktu uz
riņķa līnijas
vistuvāko punktu uz
riņķa līnijas
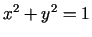 .
.
- 5.
Atrast koordinātu
sākumpunktam vistuvāko punktu uz līknes
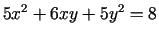 .
.
- 6.
Izmantojot Lagranža reizinātāju metodi, atrast iespējamos ekstrēma
punktus:
- 6a.
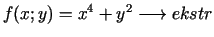 ,
, 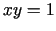 ;
;
- 6b.
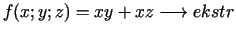 ,
, 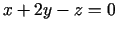 ,
, 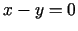 ;
;
- 6c.
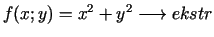 ,
, 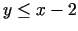 ;
;
- 6d.
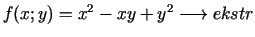 ,
,
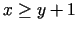 ;
;
- 6e.
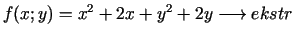 ,
,
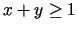 ,
, 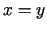 ;
;
- 6f.
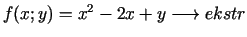 ,
,
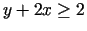 ,
, 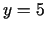 .
.
2002-05-04