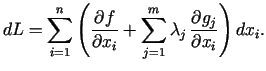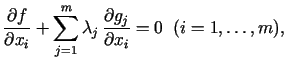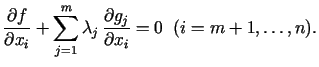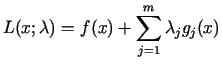Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.2.8. Uzdevumi
Augstāk: 1.2. Nosacītais ekstrēms
Iepriekšējais: 1.2.6. Lagranža reizinātāju metode, kad ierobežojumi
Kādēļ Lagranža reizinātāju metode dod labus (pareizus)
rezultātus? Lai atbildētu uz šo dabisko jautājumu, jāveic analīze.
Vēsturiski tā bija lietota tieši tāpat, kā mūsu tekstā: sākumā
praktiski, un tikai pēc kāda laika bija dots metodes pamatojums.
Sākumā aplūkosim vienkāršu gadījumu, kad minimizējamai
funkcijai ir divi argumenti un ir viens ierobežojums vienādības
formā:
Pieņemsim, ka abām funkcijām ir nepārtraukti parciālie
atvasinājumi. Ja problēmai ir atrisinājums, t.i., lokālā minimuma
punkts, kuru apzīmēsim ar
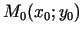 , tad kādas punkta
, tad kādas punkta
 apkārtnes šķēlumā ar pieļaujamo apgabalu
apkārtnes šķēlumā ar pieļaujamo apgabalu
 izpildās vienādība
izpildās vienādība
kur
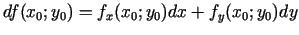 ,
bet
,
bet
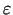 apzīmē augstākas kārtas (attiecībā pret
apzīmē augstākas kārtas (attiecībā pret 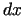 un
un
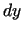 ) elementus. Tā ka
) elementus. Tā ka
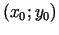 ir lokālā minimuma punkts,
tad funkcijas pieaugums
ir lokālā minimuma punkts,
tad funkcijas pieaugums
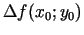 ir nenegatīvs.
Tātad
ir nenegatīvs.
Tātad
 ir vienāds ar nulli visiem pieļaujamiem
ir vienāds ar nulli visiem pieļaujamiem
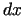 un
un 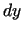 (jo pretējā gadījumā
(jo pretējā gadījumā
 un līdz ar to
un līdz ar to
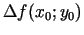 pieņemtu gan pozitīvas, gan negatīvas
vērtības). Diferencējot saiti
pieņemtu gan pozitīvas, gan negatīvas
vērtības). Diferencējot saiti  punktā
punktā 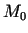 , iegūstam
pieļaujamo diferenciāļu kritēriju: pieļaujamiem
diferenciāļiem ir jāapmierina nosacījums
, iegūstam
pieļaujamo diferenciāļu kritēriju: pieļaujamiem
diferenciāļiem ir jāapmierina nosacījums
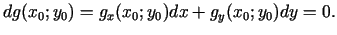 |
(1.3) |
Tātad lokālā minimuma punktā ir jāizpildās vienādojumu sistēmai:
 |
(1.4) |
-
1.13. piezīme.
- Tā kā diferenciāļi
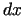 un
un 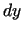 nav patvaļīgi, tad no
vienādības
nav patvaļīgi, tad no
vienādības
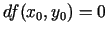 nevar secināt, ka
nevar secināt, ka
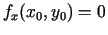 un
un
 . Piemēram,
aplūkosim problēmu:
. Piemēram,
aplūkosim problēmu:
kuras minimuma punkta koordinātas ir 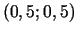 . Minimuma punktā
diferenciāļi apmierina vienādību
. Minimuma punktā
diferenciāļi apmierina vienādību
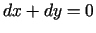 . Funkcijas
diferenciālis minimuma punktā ir
. Funkcijas
diferenciālis minimuma punktā ir
un tas, protams, ir vienāds ar nulli visiem pieļaujamiem
diferenciāļiem
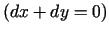 , kaut arī funkcijas
, kaut arī funkcijas
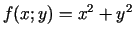 parciālie atvasinājumi minimuma punktā nav
vienādi ar nulli (
parciālie atvasinājumi minimuma punktā nav
vienādi ar nulli (
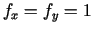 minimuma punktā).
minimuma punktā).
Lagranža ideja ir ievest pagaidām nenoteiktu parametru 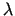 un aplūkot lielumu
un aplūkot lielumu
Tad
Tā kā
 un
un
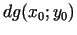 ir vienādi ar nulli,
tad
ir vienādi ar nulli,
tad 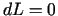 minimuma punktā. Sekojot Lagranža idejai, jāaizvēlas
tādu parametru
minimuma punktā. Sekojot Lagranža idejai, jāaizvēlas
tādu parametru 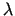 , lai viena no iekavām (teiksim, pirmā)
iepriekšējās izteiksmes pēdējā rindiņā būtu vienāda ar nulli (tas
ir iespējams, ja
, lai viena no iekavām (teiksim, pirmā)
iepriekšējās izteiksmes pēdējā rindiņā būtu vienāda ar nulli (tas
ir iespējams, ja
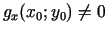 ). Tad
). Tad
Tā kā 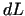 minimuma punktā ir vienāds ar nulli un diferenciālis
minimuma punktā ir vienāds ar nulli un diferenciālis
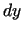 var būt izvēlēts patvaļīgi, tad koeficientam pie
var būt izvēlēts patvaļīgi, tad koeficientam pie 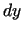 arī ir
jābūt vienādam ar nulli. Tātad
arī ir
jābūt vienādam ar nulli. Tātad
Minimuma punktā jāizpildās arī vienādībai
Nosacītā minimuma problēmā minimuma punkta noteikšanai iegūstam
trīs vienādojumu sistēmu, kura sakrīt ar sistēmu (1.4).
Tātad minimuma punkta atrašanai jārisina sistēma (1.4)
attiecībā pret 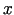 ,
,  ,
, 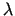 .
.
-
1.14. piezīme.
- Ja mēs no paša sākuma sastādītu funkciju
un meklētu tai brīvā ekstrēma punktu, tad iegūtu sistēmu:
Tagad aplūkosim gadījumu, kad nosacītā ekstrēma problēma ir formā:
Nepieciešamais nosacījums lokālam ekstrēmam ir vienādība
kurai jāizpildās visiem pieļaujamiem diferenciāļiem 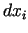 .
.
Savukārt pieļaujamiem diferenciāļiem jāapmierina
vienādības
 |
(1.5) |
Tagad reizinām (1.5) katram 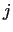 ar pagaidām
nenoteiktiem skaitļiem
ar pagaidām
nenoteiktiem skaitļiem
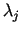 un sastādām izteiksmi
un sastādām izteiksmi
 |
(1.6) |
Ievietojot lielumu 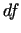 un
un 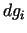 izteiksmes vienādībā
(1.6) un sagrupējot locekļus, iegūstam
izteiksmes vienādībā
(1.6) un sagrupējot locekļus, iegūstam
Lielumam 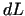 ir jābūt vienādam ar nulli visiem pieļaujamiem
diferenciāļiem
ir jābūt vienādam ar nulli visiem pieļaujamiem
diferenciāļiem 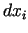 , jo
, jo 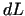 saskaņā ar (1.6) sastāv
no divām daļām, katra no kurām ir vienāda ar nulli visiem
pieļaujamiem diferenciāļiem. Tātad
saskaņā ar (1.6) sastāv
no divām daļām, katra no kurām ir vienāda ar nulli visiem
pieļaujamiem diferenciāļiem. Tātad
visiem pieļaujamiem argumentu pieaugumiem 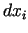 . No tiem tikai
. No tiem tikai
 diferenciāļi var būt izvēlēti patvaļīgi, jo argumentu
pieaugumi
diferenciāļi var būt izvēlēti patvaļīgi, jo argumentu
pieaugumi 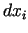 ir saistīti savā starpā ar
ir saistīti savā starpā ar  ierobežojumiem.
Izvēlēsimies Lagranža reizinātājus
ierobežojumiem.
Izvēlēsimies Lagranža reizinātājus 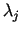
 tā, lai pirmās
tā, lai pirmās  iekavas lieluma
iekavas lieluma 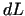 izteiksmē būtu vienādas ar
nulli. Iegūsim
izteiksmē būtu vienādas ar
nulli. Iegūsim  vienādojumu sistēmu attiecībā pret
vienādojumu sistēmu attiecībā pret
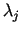 :
:
kura ir atrisināma, ja determinants
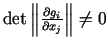 . Pārējās
. Pārējās  iekavas ir
koeficienti pie atlikušajiem
iekavas ir
koeficienti pie atlikušajiem  diferenciāļiem, kuri var būt
izvēlēti patvaļīgi, un līdz ar to šie koeficienti arī ir nulles.
Iegūsim vēl
diferenciāļiem, kuri var būt
izvēlēti patvaļīgi, un līdz ar to šie koeficienti arī ir nulles.
Iegūsim vēl  vienādojumus
vienādojumus
Visbeidzot, minimuma punktā ir jāizpildās arī ierobežojumiem
Kopā 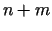 nezināmajiem
nezināmajiem
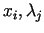
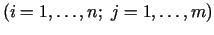 ir jāapmierina
ir jāapmierina 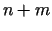 vienādojumu
sistēmu.
vienādojumu
sistēmu.
-
1.15. piezīme.
- Vienādojumu sistēmu
nezināmo
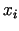 ,
,
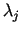 atrašanai var iegūt arī, sastādot
Lagranža funkciju
atrašanai var iegūt arī, sastādot
Lagranža funkciju
un meklējot tai brīvā ekstrēma punktu.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.2.8. Uzdevumi
Augstāk: 1.2. Nosacītais ekstrēms
Iepriekšējais: 1.2.6. Lagranža reizinātāju metode, kad ierobežojumi
2002-05-04
![]() , tad kādas punkta
, tad kādas punkta
![]() apkārtnes šķēlumā ar pieļaujamo apgabalu
apkārtnes šķēlumā ar pieļaujamo apgabalu
![]() izpildās vienādība
izpildās vienādība
![]() un aplūkot lielumu
un aplūkot lielumu
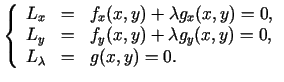
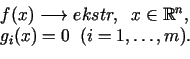
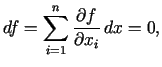
![]() un
un ![]() izteiksmes vienādībā
(1.6) un sagrupējot locekļus, iegūstam
izteiksmes vienādībā
(1.6) un sagrupējot locekļus, iegūstam