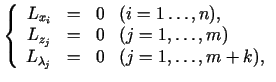Matemātika DU TSC
Nākamais: 1.2.7. Lagranža reizinātāju metodes pamatojums Augstāk: 1.2. Nosacītais ekstrēms Iepriekšējais: 1.2.5. Lagranža reizinātāju metode, kad ierobežojumi

1.2.6. Lagranža reizinātāju metode, kad ierobežojumi ir gan vienādību, gan nevienādību veidā

Kā rīkoties, ja daļa ierobežojumu ir vienādību veidā un daļa - nevienādību veidā? Aplūkosim problēmu:

$$f(x)\rightarrow ekstr,\;\;x\in\mathbb{R}^n,$$

$$g_{i}(x)\leq\;\;(i=1,\ldots ,m),$$

$$h_{j}(x)=0,\;\;(j=1,\ldots,k).$$

Risināšanas shēma.

Ievedīsim 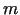$m$ fiktīvus mainīgos 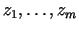$z_1,\ldots,z_m$ (tie līdzsvaro ierobežojumus nevienādību veidā):

$$g_{i}(x)+z_{i}^{2}=0\;\;(i=1,\ldots,m).$$

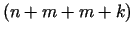Tālāk jāminimizē funkciju $f$ pie nosacījumiem vienādību veidā. Sastādām Lagranža $(n+m+m+k)$ argumentu funkciju formā

$$L(x,z,\lambda)=f(x)+\sum\limits_{i = 1}^m{\lambda_i (g_i (x) + z_i^2 )} + \sum\limits_{j = 1}^k{\lambda_{m + j}h_j (x)}$$

un atrodam tās stacionāros punktus. Tātad problēmas atrisinājumi, ja tie eksistē, atrodas starp 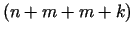$(n+m+m+k)$ vienādojumu sistēmas

$$\left\{\begin{array}{cccl} L_{x_i}&=&0&(i=1\ldots,n), \ L_{z_j}&=&0&(j=1,\ldots,m)\ L_{\lambda _j}&=&0&(j=1,\ldots,m + k), \end{array}\right.$$

atrisinājumiem.

Matemātika DU TSC
Nākamais: 1.2.7. Lagranža reizinātāju metodes pamatojums Augstāk: 1.2. Nosacītais ekstrēms Iepriekšējais: 1.2.5. Lagranža reizinātāju metode, kad ierobežojumi