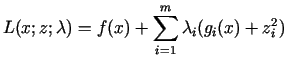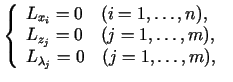Matemātika DU TSC
Nākamais: 1.2.6. Lagranža reizinātāju metode, kad ierobežojumi Augstāk: 1.2. Nosacītais ekstrēms Iepriekšējais: 1.2.4. Lagranža reizinātāju metode, kad ierobežojumi

1.2.5. Lagranža reizinātāju metode, kad ierobežojumi ir nevienādību veidā

Paskaidrosim Lagranža metodes būtību šajā gadījumā ar piemēru palīdzību.

1.5. piemērs.  [Divi argumenti, viens ierobežojums]

$\phantom{\/}$

Minimizēt funkciju $f(x;y)=x^{2}+y^{2}$ pie nosacījuma $x+y\geq 1$.

Mēģināsim atrast minimuma punktu, lietojot Lagranža reizinātāju metodi. Ievedīsim fiktīvu mainīgo $z$ un ar tā palīdzību līdzsvarosim ierobežojumu $x+y\geq 1$, pārrakstot to vienādības veidā:

$$x+y=1+z^{2}.$$

Tagad jāminimizē funkcija $f$, ja nosacījums ir vienādības veidā. Sastādīsim Lagranža funkciju formā

$$L(x;y;z;\lambda)=f(x;y)+\lambda(x+y-z^{2}-1)$$

un atradīsim tās stacionāros punktus. Risinot vienādojumu sistēmu

$$\left\{\begin{array}{ccl} L_{x}&=&2x+\lambda=0,\ L_{y}&=&2y+\la... ...=0,\ L_{z}&=&-2z\lambda=0,\ L_{\lambda}&=&x+y-z^{2}-1=0, \end{array}\right.$$

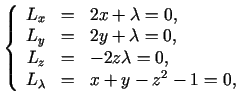iegūsim $x$, $y$, $z$ un $\lambda$ vērtības:

$$x = 0,5,\;\;y = 0,5,\;\;z = 0,\;\;\lambda=-1.$$

Tātad nosacītā ekstrēma punkts (no ģeometriskā viedokļa ir skaidrs, ka tas ir minimuma punkts) ir punkts $(0,5; 0,5)$. Pie šī paša secinājuma varēja nonākt, izmantojot tikai ģeometriskus spriedumus. 1.4. zīmējumā ir attēlota $(x;y)$-plakne, taisne $AB$, kuras vienādojums ir $x+y=1$, un divas funkcijas $f$ līmeņlīnijas. Atgādināsim, ka par funkcijas līmeņlīnijām sauc līnijas, uz kurām dotās funkcijas vērtības ir konstantas. Pieņemsim, ka līmeņlīnija $C_{1}$ pieskaras taisnei $AB$. Pieskaršanās punkta koordinātas ir $(0,5; 0,5)$. No ģeometriskā viedokļa ir skaidrs, ka tieši līmeņlīnijas $C_{1}$ un taisnes $AB$ pieskarpunkts ir dotās problēmas atrisinājums.

1.4. zīm. Funkcijas $f(x;y)=x^2+y^2$ līmeņlīnijas $x^2+y^2=C_1$ un $x^2+y^2=C$ un taisne $AB$ ar vienādojumu $x+y=1$, kura pieskaras pirmajai līmeņlīnijai.

1.11. piezīme. 

Fakts, ka $z$ vērtība ir nulle, norāda uz to, ka ekstrēma punkts atrodas uz pieļaujamā apgabala robežas, kur izpildās vienādība $x+y=1$.

Risināšanas shēma.

Aplūkosim vairāku argumentu funkcijas $f(x)$, $x\in\mathbb{R}^{n}$, minimizēšanas problēmu, kad ir uzdoti $m$ ierobežojumi nevienādību veidā:

$$g_{i}(x)\leq 0\;\;(i=1,\ldots,m).$$

Ievedīsim $m$ fiktīvus mainīgos $z_1,\ldots,z_m$ (tie līdzsvaro ierobežojumus nevienādību veidā):

$$g_{i}(x)+z_{i}^{2}=0\;\;(i=1,\ldots,m).$$

Tālāk jāminimizē funkciju $f$ pie nosacījumiem vienādību veidā. Sastādām Lagranža $(n+2m)$ argumentu funkciju formā

$$L(x;z;\lambda)=f(x)+\sum\limits_{i = 1}^m\lambda_i (g_i (x)+z_i^2)$$

un atrodam tās stacionāros punktus. Tātad problēmas atrisinājumi atrodas starp $(n+2m)$ vienādojumu sistēmas

$$\left\{\begin{array}{l} L_{x_i}=0\quad (i=1,\ldots,n),\ L_{z_j}... ...ad (j=1,\ldots,m),\ L_{\lambda_j}=0\quad (j =1,\ldots,m), \end{array}\right.$$

atrisinājumiem.

1.12. piezīme. 

Atšķirībā no gadījuma, kad ierobežojumi ir vienādību formā un kad, kā jau tika iepriekš minēts, nav jēgas aplūkot problēmas, kurās ierobežojumu skaits $m$ ir lielāks vai vienāds ar mainīgo skaitu $n$, problēmas, kurās ierobežojumi ir nevienādību formā, var būt saturīgas arī tad, ja ierobežojumu skaits $m$ ir lielāks par minimizējamas funkcijas $f$ argumentu skaitu $n$. Iedomājieties, piemēram, regulāru sešstūri ar centru punktā $(0;0)$, tā iekšieni kā pieļaujamo apgabalu (ko var uzdot ar $6$ ierobežojumiem nevienādību formā) un aplūkojiet funkcijas $f(x;y)=x^{2}+y^{4}$ (argumentu skaits $n = 2$) minimizēšanas problēmu (sešstūri var arī aizvietot ar $m$-stūri).

Matemātika DU TSC
Nākamais: 1.2.6. Lagranža reizinātāju metode, kad ierobežojumi Augstāk: 1.2. Nosacītais ekstrēms Iepriekšējais: 1.2.4. Lagranža reizinātāju metode, kad ierobežojumi