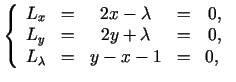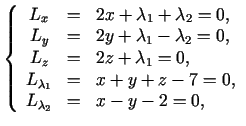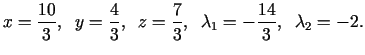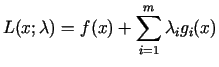Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.2.5. Lagranža reizinātāju metode, kad ierobežojumi
Augstāk: 1.2. Nosacītais ekstrēms
Iepriekšējais: 1.2.3. Mainīgo izslēgšanas metode
1.2.4. Lagranža reizinātāju metode, kad
ierobežojumi ir vienādību veidā
Mainīgo izslēgšanas metode ne vienmēr ir ērta, jo dažkārt
argumentu izslēgšana prasa vienādojumu un vienādojumu sistēmu
analītisku risinājumu, kas, vispārīgi runājot, ir
iespējams tikai retos gadījumos.
Nosaukumā
minētā metode dodiespēju sākotnējo nosacītā minimuma problēmu
reducēt uz brīvā ekstrēma problēmu.
-
1.3. piemērs. [Divi argumenti, viens ierobežojums]
-

Minimizēt funkciju
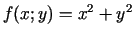 , ja
, ja
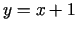 .
.
Funkcijas  grafiks ir eliptiskais
paraboloīds, un
grafiks ir eliptiskais
paraboloīds, un  un
un 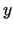 vērtības atrodas uz taisnes
vērtības atrodas uz taisnes 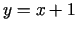 divdimensiju telpā
divdimensiju telpā
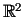 . No ģeometriskā viedokļa ir
skaidrs, ka minimuma punktam ir jāeksistē.
. No ģeometriskā viedokļa ir
skaidrs, ka minimuma punktam ir jāeksistē.
Saskaņā
ar Lagranža metodi ir jāieved vienu (pēc ierobežojumu skaita!)
parametru 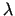 un jāsastāda tā saucamā Lagranža
funkcija
un jāsastāda tā saucamā Lagranža
funkcija
Tālāk jāmeklē Lagranža funkcijas stacionārie punkti ar ieceri, ka
tie dos sākotnējās problēmas atrisinājumu. Lagranža funkcijas
stacionārie punkti apmierina vienādojumu sistēmu
kuras atrisinājums ir 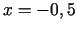 ,
, 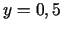 ,
,
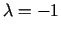 .
.
-
1.9. piezīme.
- Nav jēgas aplūkot divu argumentu funkcijas
minimizēšanas problēmu pie diviem ierobežojumiem, jo
divi ierobežojumi, vispārīgi runājot, nosaka vienīgo punktu, un
tad minimizēšanas problēma kļūst triviāla. Tā, piemēram,
iepriekš aplūkotā problēma ar papildnosacījumu
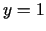 reducējas uz funkcijas
reducējas uz funkcijas 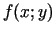 minimizēšanas problēmu
kopā
minimizēšanas problēmu
kopā
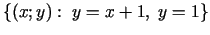 , kura sastāv, acīmredzot, no
vienīgā punkta
, kura sastāv, acīmredzot, no
vienīgā punkta 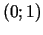 .
.
-
1.4. piemērs. [Trīs argumenti, divi ierobežojumi]
-

Minimizēt funkciju
ja
Sastādām Lagranža
Tā kā ir divi ierobežojumi, tad tiek ievesti divi Lagranža
reizinātāji
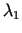 un
un
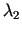 jeb Lagranža
vektors
jeb Lagranža
vektors
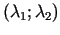 . Tālāk ir jārisina standarta
brīvā ekstrēma problēma. Lagranža funkcijas stacionārie punkti
apmierina vienādojumu sistēmu
. Tālāk ir jārisina standarta
brīvā ekstrēma problēma. Lagranža funkcijas stacionārie punkti
apmierina vienādojumu sistēmu
kuras atrisinājums ir:
Tātad nosacītā ekstrēma punkts (no ģeometriskā viedokļa ir
skaidrs, ka tas ir minimuma punkts) ir punkts
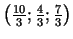 .
.
-
1.10. piezīme.
- Risinot vienādojumu sistēmu, var neinteresēties (pagaidām) par
Lagranža reizinātāju vērtībām.
- Risināšanas shēma.
- Aplūkosim vairāku argumentu funkcijas
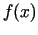 ,
,
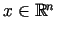 , minimizēšanas problēmu, kad ir uzdoti
, minimizēšanas problēmu, kad ir uzdoti 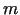
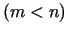 ierobežojumi vienādību veidā:
ierobežojumi vienādību veidā:
Jāsastāda 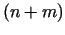 argumentu Lagranža funkcija
argumentu Lagranža funkcija
un jāaplūko brīva ekstrēma problēma šai Lagranža funkcijai. Tātad,
problēmas atrisinājumi atrodas starp 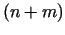 vienādojumu sistēmas
vienādojumu sistēmas
atrisinājumiem.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.2.5. Lagranža reizinātāju metode, kad ierobežojumi
Augstāk: 1.2. Nosacītais ekstrēms
Iepriekšējais: 1.2.3. Mainīgo izslēgšanas metode
2002-05-04
![]() , ja
, ja
![]() .
.