


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.2.4. Lagranža reizinātāju metode, kad ierobežojumi
Augstāk: 1.2. Nosacītais ekstrēms
Iepriekšējais: 1.2.2. Definīcijas
Mainīgo izslēgšanas metode faktiski jau tika lietota, risinot
iepriekšējā apakšparagrāfā apskatītās problēmas. Metodes
ideja ir izslēgt daļu no argumentiem, izmantojot ierobežojumus, un
risināt minimuma problēmu bez ierobežojumiem. Iepriekšējā piemērā
par virsmas laukuma minimumu mainīgais 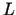 tika izslēgts no
virsmas laukuma
tika izslēgts no
virsmas laukuma 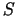 formulas un lielums
formulas un lielums 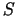 kļuva par viena reāla
argumenta funkciju.
kļuva par viena reāla
argumenta funkciju.
Minimizējot vairāku
argumentu funkciju 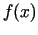 , kur
, kur
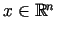 , un
, un
mainīgo izslēgšanas metode, vispārīgi runājot, nozīmē, ka 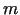 argumenti (teiksim,
argumenti (teiksim,
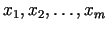 ) tiek izteikti ar
pārējiem mainīgajiem
) tiek izteikti ar
pārējiem mainīgajiem
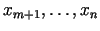 :
:
un pēc to ievietošanas funkcijas  formulā iegūstam
formulā iegūstam 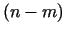 argumentu funkciju
argumentu funkciju
kurai meklējam brīvo minimumu.
Noteiktības
labad visur runa ir par minimumu, bet viss teiktais attiecas arī
uz maksimizēšanas problēmām.
-
1.8. piezīme.
- Netriviāls ir jautājums, kad daļu argumentu (teiksim,
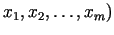 var izteikt ar pārējiem mainīgajiem
var izteikt ar pārējiem mainīgajiem
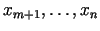 kādā punkta
kādā punkta 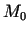 apkārtnē. No matemātiskas
analīzes kursa ir zināms [7, 208. lpp.], ka tas ir
iespējams, ja visi
apkārtnē. No matemātiskas
analīzes kursa ir zināms [7, 208. lpp.], ka tas ir
iespējams, ja visi 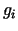 un
un
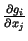 ir
nepārtraukti un
ir
nepārtraukti un
punkta 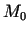 apkārtnē.
apkārtnē.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.2.4. Lagranža reizinātāju metode, kad ierobežojumi
Augstāk: 1.2. Nosacītais ekstrēms
Iepriekšējais: 1.2.2. Definīcijas
2002-05-04
![]() tika izslēgts no
virsmas laukuma
tika izslēgts no
virsmas laukuma ![]() formulas un lielums
formulas un lielums ![]() kļuva par viena reāla
argumenta funkciju.
kļuva par viena reāla
argumenta funkciju.
