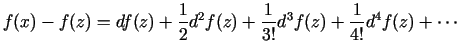Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.1.6. Problēmas par peļņas maksimumu atrisinājums
Augstāk: 1.1. Brīvais ekstrēms
Iepriekšējais: 1.1.4. Stacionārie punkti problēmā par peļņas
1.1.5. Ekstrēma pietiekamie nosacījumi
Dažreiz stacionārā punkta raksturs ir skaidrs no minimuma
definīcijas. Piemēram, funkcijai
punkts 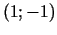 ir minimuma punkts, jo pārējos punktos funkcija
ir minimuma punkts, jo pārējos punktos funkcija
 ir pozitīva. Citos, ne tik acīmredzamos gadījumos, ir vēlams
iegūt ekstrēma pazīmi.
ir pozitīva. Citos, ne tik acīmredzamos gadījumos, ir vēlams
iegūt ekstrēma pazīmi.
Pieņemsim, ka
funkcijai  ir nepārtraukti parciālie atvasinājumi pēc
ir nepārtraukti parciālie atvasinājumi pēc
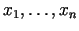 līdz otrai kārtai
ieskaitot.
līdz otrai kārtai
ieskaitot.
-
1.2. teorēma.
- Ja funkcijas
 stacionārajā punktā
stacionārajā punktā  tās diferenciālis
tās diferenciālis
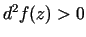 (t.i., kvadrātiskā forma
(t.i., kvadrātiskā forma
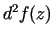 ir pozitīva), tad punkts
ir pozitīva), tad punkts  ir funkcijas
ir funkcijas  (lokālā)
minimuma punkts.
(lokālā)
minimuma punkts.
 Funkcijas
Funkcijas  pieaugumam punktā
pieaugumam punktā  ir spēkā formula (Teilora
rinda diferenciālā formā) [7, 195. lpp.]
ir spēkā formula (Teilora
rinda diferenciālā formā) [7, 195. lpp.]
kur trešais elements labajā pusē ir augstākas kārtas bezgalīgi
mazs lielums salīdzinot ar
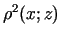 , ja
, ja
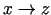 .
Tā kā saskaņā ar pieņēmumu
.
Tā kā saskaņā ar pieņēmumu  ir funkcijas
ir funkcijas 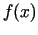 stacionārs
punkts, tad
stacionārs
punkts, tad 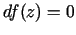 . Tas nozīmē, ka starpības
. Tas nozīmē, ka starpības
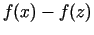 zīme
zīme  vērtībām no pietiekami mazas punkta
vērtībām no pietiekami mazas punkta  apkārtnes ir
atkarīga no diferenciāļa
apkārtnes ir
atkarīga no diferenciāļa 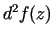 zīmes. Tāpēc
zīmes. Tāpēc
ja punkts  ir pietiekami tuvs
ir pietiekami tuvs  punktam. No minimuma
definīcijas seko, ka punkts
punktam. No minimuma
definīcijas seko, ka punkts  ir funkcijas
ir funkcijas  (lokālā) minimuma
punkts.
(lokālā) minimuma
punkts.
- 1. secinājums.
- Ja funkcijas
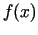 stacionārā punktā
stacionārā punktā  diferenciālis
diferenciālis
tad  ir funkcijas
ir funkcijas 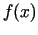 (lokālā) maksimuma punkts. Lai to
pierādītu, ir pietiekami aplūkot funkciju
(lokālā) maksimuma punkts. Lai to
pierādītu, ir pietiekami aplūkot funkciju 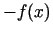 , kurai otrās
kārtas diferenciālis ir nenegatīvs, un tad pielietot
1.2. teorēmu.
, kurai otrās
kārtas diferenciālis ir nenegatīvs, un tad pielietot
1.2. teorēmu.
1.2. teorēmas un 1. secinājuma pielietošanai stacionārā
punkta rakstura pētīšanā ir nepieciešama prasme rēķināt otrās
kārtas diferenciāli dotajā punktā.
Divu
argumentu funkcijas
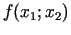 otrās kārtas diferenciāli
dotajā punktā
otrās kārtas diferenciāli
dotajā punktā
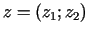 aprēķina šādi:
aprēķina šādi:
kur
Tātad diferenciālis 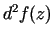 ir kvadrātiska forma attiecībā pret
mainīgajiem
ir kvadrātiska forma attiecībā pret
mainīgajiem
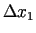 un
un
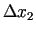 . Parciālie
atvasinājumi tiek aprēķināti punktā
. Parciālie
atvasinājumi tiek aprēķināti punktā  .
.
Apzīmējot parciālos atvasinājumus:
apskatīsim kvadrātisku matricu
No matemātiskas analīzes kursa ir zināms, ka jauktie atvasinājumi
ir vienādi savā starpā, ja tie ir nepārtraukti [7, 5. nodaļa, §
4], tāpēc
No kvadrātisko formu teorijas ir zināms [7, 198. lpp.]:
- ja
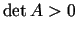 un
un
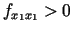 , tad kvadrātiskā forma ir pozitīva;
, tad kvadrātiskā forma ir pozitīva;
- ja
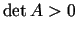 un
un
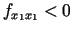 , tad kvadrātiskā forma ir negatīva;
, tad kvadrātiskā forma ir negatīva;
- ja
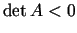 , tad kvadrātiskā forma pieņem gan pozitīvas, gan negatīvas
vērtības.
, tad kvadrātiskā forma pieņem gan pozitīvas, gan negatīvas
vērtības.
Formulēsim divu argumentu funkcijas ekstrēma punktu
meklēšanas shēmu:
- atrast stacionārus punktus, risinot sistēmu (1.1);
- katrā stacionārā punktā noteikt determinanta
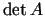 zīmi;
zīmi;
- ja stacionārā punktā
 ir spēkā
ir spēkā
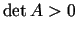 un
un
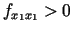 , tad
, tad
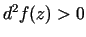 un
un  ir (stingrā) minimuma punkts;
ir (stingrā) minimuma punkts;
- ja stacionārajā punktā
 ir spēkā
ir spēkā
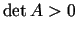 un
un
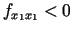 , tad
, tad
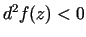 un
un  ir (stingrā) maksimuma punkts;
ir (stingrā) maksimuma punkts;
- ja stacionārajā punktā
 ir spēkā
ir spēkā
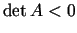 , tad
, tad
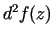 pieņem gan pozitīvas, gan negatīvas vērtības kādā
punkta
pieņem gan pozitīvas, gan negatīvas vērtības kādā
punkta  apkārtnē un
apkārtnē un  nav ekstrēma punkts;
nav ekstrēma punkts;
- ja stacionārajā punktā
 ir spēkā
ir spēkā
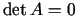 , tad ir
nepieciešama tālāka analīze.
, tad ir
nepieciešama tālāka analīze.
-
1.7. piezīme.
- 6. gadījumā, kad
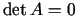 ,
stacionārā punkta
,
stacionārā punkta  rakstura analīze var būt saistīta ar
augstākas kārtas diferenciāļu rēķināšanu, protams, ja funkcijai
eksistē attiecīgās kārtas atvasinājumi. Tiešām,
rakstura analīze var būt saistīta ar
augstākas kārtas diferenciāļu rēķināšanu, protams, ja funkcijai
eksistē attiecīgās kārtas atvasinājumi. Tiešām,
un starpības zīme vienādības kreisajā pusē ir atkarīga no pirmā no
nulles atšķirīgā diferenciāļa vienādības labajā pusē.
Apskatīsim dažus piemērus saistībā ar iepriekšējo piezīmi.
-
1.1. piemērs.
- Apskatīsim funkciju
Punkts 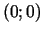 ir funkcijas
ir funkcijas  stacionārs punkts, jo šajā punktā
diferenciāļi
stacionārs punkts, jo šajā punktā
diferenciāļi 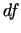 un
un 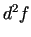 ir vienādi ar nulli. Tai
pašā laikā
ir vienādi ar nulli. Tai
pašā laikā
Tā kā funkcija  jebkurā punkta
jebkurā punkta 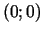 apkārtnē pieņem abu
zīmju vērtības, tad funkcijai
apkārtnē pieņem abu
zīmju vērtības, tad funkcijai  punktā
punktā 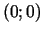 ekstrēma nav.
ekstrēma nav.
-
1.2. piemērs.
- Apskatīsim funkciju
Punkts 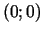 ir funkcijas
ir funkcijas  stacionārs punkts. Šajā punktā
stacionārs punkts. Šajā punktā
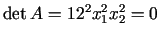 un, lai noskaidrotu stacionārā
punkta raksturu, ir nepieciešama tālāka pētīšana. Var pārbaudīt,
ka
un, lai noskaidrotu stacionārā
punkta raksturu, ir nepieciešama tālāka pētīšana. Var pārbaudīt,
ka 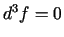 punktā
punktā 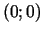 , bet
, bet
ir pozitīva forma. Tādējādi punkts 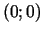 ir funkcijas
ir funkcijas  minimuma punkts.
minimuma punkts.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.1.6. Problēmas par peļņas maksimumu atrisinājums
Augstāk: 1.1. Brīvais ekstrēms
Iepriekšējais: 1.1.4. Stacionārie punkti problēmā par peļņas
2002-05-04
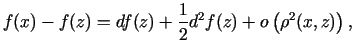
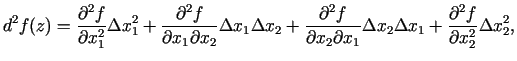
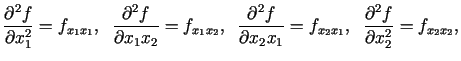
![$\displaystyle A=\left[\begin{array}{cc} f_{x_1 x_1}&f_{x_1 x_2}\ f_{x_2 x_1}&f_{x_2 x_2} \end{array}\right].$](img122.gif)