


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.1.7. Uzdevumi
Augstāk: 1.1. Brīvais ekstrēms
Iepriekšējais: 1.1.5. Ekstrēma pietiekamie nosacījumi
1.1.6. Problēmas par peļņas maksimumu atrisinājums
Noskaidrosim stacionārā punkta 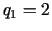 ,
, 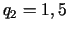 raksturu
problēmā par peļņas maksimimumu. Tā kā
raksturu
problēmā par peļņas maksimimumu. Tā kā
tad punkts 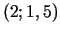 ir ekstrēma punkts. Tā kā
ir ekstrēma punkts. Tā kā
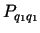 ir
negatīvs, bet
ir
negatīvs, bet 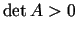 , tad apskatāmais punkts ir minimuma
punkts. Noteiksim cenas
, tad apskatāmais punkts ir minimuma
punkts. Noteiksim cenas 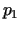 un
un 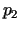 , pēc kurām ir jāpārdod
preces katrā tirgū, lai iegūtu maksimālo peļņu:
, pēc kurām ir jāpārdod
preces katrā tirgū, lai iegūtu maksimālo peļņu:
2002-05-04
![]() ,
, ![]() raksturu
problēmā par peļņas maksimimumu. Tā kā
raksturu
problēmā par peļņas maksimimumu. Tā kā