


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.2. Nosacītais ekstrēms
Augstāk: 1.1. Brīvais ekstrēms
Iepriekšējais: 1.1.6. Problēmas par peļņas maksimumu atrisinājums
- 1.
Monopolists nosaka preču cenas divos tirgos. Tirgū A pieprasījuma funkcija
(sakarība starp cenu un daudzumu) ir
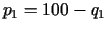 , tirgū B
attiecīgi
, tirgū B
attiecīgi
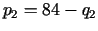 , kur
, kur 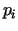 - cenas,
- cenas, 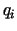 -
daudzumi. Izdevumus izsaka funkcija
-
daudzumi. Izdevumus izsaka funkcija
Cik daudz preču (un par kādām cenām) jāpardod katrā tirgū, lai
peļņa būtu maksimālā?
- 2.
Noteikt funkcijas
stacionāros punktus un to raksturu.
- 3.
Atrast stacionāros punktus un noteikt to raksturu:
- 3a.
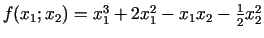 ;
;
- 3b.
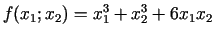 ;
;
- 3c.
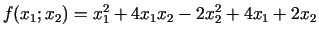 ;
;
- 3d.
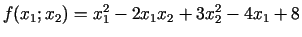 .
.
2002-05-04