Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.1.5. Ekstrēma pietiekamie nosacījumi
Augstāk: 1.1. Brīvais ekstrēms
Iepriekšējais: 1.1.3. Ekstrēma eksistences nepieciešamie nosacījumi
Problēmā par peļņas maksimumu funkcijas
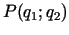 stacionāro punktu noteikšanai risinām vienādojumu sistēmu
stacionāro punktu noteikšanai risinām vienādojumu sistēmu
Atrisinājums: 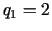 ,
, 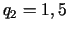 . Tātad stacionāro punktu kopa
sastāv no viena punkta. Ja pēc problēmas satura var spriest, ka
funkcijai
. Tātad stacionāro punktu kopa
sastāv no viena punkta. Ja pēc problēmas satura var spriest, ka
funkcijai 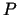 ir maksimums, tad var secināt, ka maksimuma punkts
sakrīt ar vienīgo stacionāro punktu.
ir maksimums, tad var secināt, ka maksimuma punkts
sakrīt ar vienīgo stacionāro punktu.
-
1.6. piezīme.
- Stacionārs punkts var nebūt ekstrēma
punkts. Piemēram, punkts
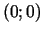 ir vienīgais funkcijas
ir vienīgais funkcijas
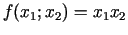 stacionārais punkts. Jebkurā šī punktā
apkārtnē funkcija
stacionārais punkts. Jebkurā šī punktā
apkārtnē funkcija  pieņem gan pozitīvas, gan negatīvas
vērtības. Tāpēc punkts
pieņem gan pozitīvas, gan negatīvas
vērtības. Tāpēc punkts 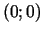 nav ne maksimuma, ne minimuma
punkts.
nav ne maksimuma, ne minimuma
punkts.
No iepriekšējās piezīmes seko, ka ir svarīgi atrast tādus
nosacījumus, kuri ļautu noteikt, vai dotais stacionārais punkts ir
minimuma vai maksimuma punkts.
2002-05-04
![]() stacionāro punktu noteikšanai risinām vienādojumu sistēmu
stacionāro punktu noteikšanai risinām vienādojumu sistēmu