


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.1.4. Stacionārie punkti problēmā par peļņas
Augstāk: 1.1. Brīvais ekstrēms
Iepriekšējais: 1.1.2. Definīcijas
Apskatīsim telpas 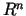 vaļēju
apakškopu
vaļēju
apakškopu 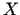 (speciālgadījumā
(speciālgadījumā
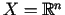 ).
Pieņemsim, ka funkcijai
).
Pieņemsim, ka funkcijai
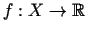 ir lokāls
minimums kopas
ir lokāls
minimums kopas 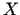 punktā
punktā
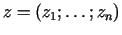 , t.i.,
, t.i.,
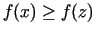 visiem
visiem  no kādas punkta
no kādas punkta  apkārtnes.
apkārtnes.
-
1.1. teorēma.
- Ja funkcijai
 kopā
kopā 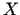 eksistē nepārtraukti
pirmās kārtas parciālie atvasinājumi pēc visiem
eksistē nepārtraukti
pirmās kārtas parciālie atvasinājumi pēc visiem 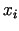 , tad
funkcijas
, tad
funkcijas  minimuma punktā
minimuma punktā  funkcijas
funkcijas  diferenciālis ir
vienāds ar nulli.
diferenciālis ir
vienāds ar nulli.
 Funkcijas
Funkcijas  pieaugumam punktā
pieaugumam punktā  ir spēkā formula
[7, 179. lpp.]
ir spēkā formula
[7, 179. lpp.]
Abi saskaitāmie labajā pusē tiecas uz nulli, ja
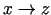 ,
bet otrais saskaitāmais ir bezgalīgi mazs augstākas kārtas lielums
nekā
,
bet otrais saskaitāmais ir bezgalīgi mazs augstākas kārtas lielums
nekā
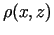 , t.i.,
, t.i.,
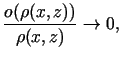 ja ja 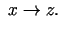 |
|
Tātad starpības 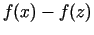 zīmi, kad
zīmi, kad  ir pietiekami tuvs
ir pietiekami tuvs  ,
nosaka diferenciāļa
,
nosaka diferenciāļa 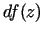 zīme.
zīme.
Pieņemsim, ka kāds parciālais atvasinājums punktā  nav vienāds
ar nulli. Noteiktības labad pieņemsim, ka
nav vienāds
ar nulli. Noteiktības labad pieņemsim, ka
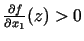 . Aplūkosim punktu
. Aplūkosim punktu
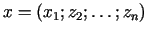 , kurā
, kurā
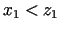 . Ja
. Ja  ir
pietiekami tuvs
ir
pietiekami tuvs 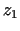 , tad
, tad
kas ir pretrunā nosacījumam par lokālo minimumu punktā
 .
.
Līdzīgi var pierādīt, ka pārējie
parciālie atvasinājumi punktā  arī ir vienādi ar nulli.
arī ir vienādi ar nulli.
Visu parciālo atvasinājumu vienādība ar nulli punktā  nozīmē,
ka diferenciālis
nozīmē,
ka diferenciālis 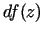 ir vienāds ar
nulli.
ir vienāds ar
nulli.
-
1.4. piezīme.
- Pierādītais apgalvojums praktiski nozīmē to, ka, lai atrastu
funkcijas
 minimuma punktus, ir jāatrisina vienādojumu sistēma
minimuma punktus, ir jāatrisina vienādojumu sistēma
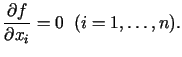 |
(1.1) |
-
1.5. piezīme.
- Maksimuma punktu koordinātām arī ir
jāapmierina sistēma (1.1), jo maksimuma problēmu
var reducēt uz minimuma problēmu, mainot funkcijas
 zīmi uz
pretējo. Tātad, lai funkcijai
zīmi uz
pretējo. Tātad, lai funkcijai  punktā
punktā  eksistētu ekstrēms,
ir nepieciešams, lai
eksistētu ekstrēms,
ir nepieciešams, lai
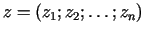 apmierinātu sistēmu (1.1).
apmierinātu sistēmu (1.1).
Sistēmas (1.1) atrisinājumus sauc par
funkcijas  stacionāriem punktiem.
stacionāriem punktiem.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.1.4. Stacionārie punkti problēmā par peļņas
Augstāk: 1.1. Brīvais ekstrēms
Iepriekšējais: 1.1.2. Definīcijas
2002-05-04
![]() vaļēju
apakškopu
vaļēju
apakškopu ![]() (speciālgadījumā
(speciālgadījumā
![]() ).
Pieņemsim, ka funkcijai
).
Pieņemsim, ka funkcijai
![]() ir lokāls
minimums kopas
ir lokāls
minimums kopas ![]() punktā
punktā
![]() , t.i.,
, t.i.,
![]() visiem
visiem ![]() no kādas punkta
no kādas punkta ![]() apkārtnes.
apkārtnes.
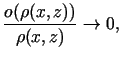 ja
ja 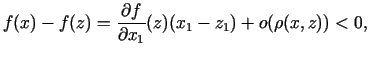
![]() stacionāriem punktiem.
stacionāriem punktiem.