


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.1.3. Ekstrēma eksistences nepieciešamie nosacījumi
Augstāk: 1.1. Brīvais ekstrēms
Iepriekšējais: 1.1.1. Problēma par peļņas maksimumu
Atgādināsim, ka par
funkciju
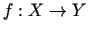 sauc attēlojumu, kurā katram
elementam
sauc attēlojumu, kurā katram
elementam 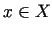 atbilst pilnīgi noteikts elements
atbilst pilnīgi noteikts elements 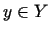 ,
kuru apzīmē ar
,
kuru apzīmē ar 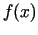 un sauc par elementa
un sauc par elementa  attēlu
attēlojumā
attēlu
attēlojumā  . Speciālgadījumā
. Speciālgadījumā 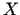 un
un 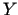 var būt viena un tā
pati kopa. Aktuāls ir gadījums, kad kopa
var būt viena un tā
pati kopa. Aktuāls ir gadījums, kad kopa 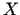 ir vienāda ar Eiklīda
telpu
ir vienāda ar Eiklīda
telpu
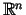 vai kādu tās apakškopu, bet kopa
vai kādu tās apakškopu, bet kopa 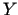 ir
vienāda ar reālo skaitļu kopu
ir
vienāda ar reālo skaitļu kopu
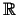 .
.
Telpas
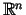 elementus
elementus
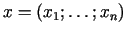 sauc
arī par šīs telpas punktiem. Ja
sauc
arī par šīs telpas punktiem. Ja
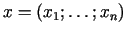 ,
tad reālos skaitļus
,
tad reālos skaitļus 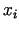
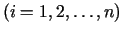 sauc par
punkta
sauc par
punkta  koordinātām. Gadījumos, kad
koordinātām. Gadījumos, kad 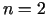 vai
vai 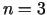 ,
telpas
,
telpas
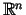 punktu var viegli attēlot
ģeometriski.
punktu var viegli attēlot
ģeometriski.
Par attālumu starp
telpas
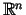 punktiem
punktiem
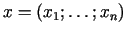 un
un
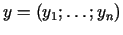 sauc lielumu
sauc lielumu
Par vaļēju lodi ar centru punktā
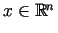 un
rādiusu
un
rādiusu 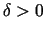 sauc telpas
sauc telpas
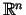 apakškopu
apakškopu
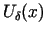 , kas sastāv no visiem tiem un tikai tiem punktiem
, kas sastāv no visiem tiem un tikai tiem punktiem
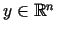 , kuru attālums
, kuru attālums 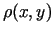 līdz punktam
līdz punktam  ir
mazāks nekā skaitlis
ir
mazāks nekā skaitlis 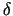 , t.i.,
, t.i.,
No ģeometriskā viedokļa, ja 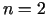 , tad
, tad
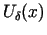 ir riņķis
ar centru dotajā punktā
ir riņķis
ar centru dotajā punktā  un rādiusu
un rādiusu 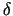 , bet, ja
, bet, ja 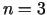 ,
tad
,
tad
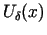 ir lode ar centru dotajā punktā
ir lode ar centru dotajā punktā  un rādiusu
un rādiusu
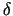 .
.
Par punkta
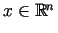 apkārtni sauc jebkuru telpas
apkārtni sauc jebkuru telpas
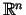 apakškopu, kas satur vismaz vienu vaļēju lodi
apakškopu, kas satur vismaz vienu vaļēju lodi
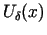 .
Protams, vaļēja lode
.
Protams, vaļēja lode
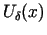 arī ir punkta
arī ir punkta  apkārtne.
apkārtne.
Punktu
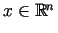 sauc par
kopas
sauc par
kopas
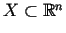 iekšēju punktu, ja eksistē
šī punkta apkārtne, kas iekļaujas kopā
iekšēju punktu, ja eksistē
šī punkta apkārtne, kas iekļaujas kopā 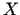 (skat.
1.1. zīm.).
(skat.
1.1. zīm.).
-
1.1. piezīme.
- Gadījumā, kad
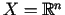 , jebkurš punkts
, jebkurš punkts
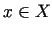 ir kopas
ir kopas 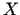 iekšējais punkts.
iekšējais punkts.
Kopu
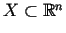 sauc par vaļēju kopu, ja
jebkurš tās punkts ir iekšējais.
sauc par vaļēju kopu, ja
jebkurš tās punkts ir iekšējais.
Ja
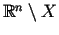 (- kopas
(- kopas 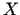 papildkopa telpā
papildkopa telpā
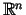 ) ir vaļēja kopa, tad kopu
) ir vaļēja kopa, tad kopu 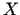 sauc par
slēgtu kopu.
sauc par
slēgtu kopu.
-
1.2. piezīme.
- Meklējot funkciju ekstrēmus (minimumus un
maksimumus), jāizšķir divi svarīgi gadījumi, proti, vai ekstrēms
tiek meklēts vaļējā vai slēgtā kopā. Tas ir atkarīgs no problēmas
formulējuma.
Saka, ka kopā
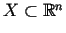 definētai funkcijai
definētai funkcijai  ir
lokāls minimums punktā
ir
lokāls minimums punktā 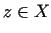 , ja eksistē tāda punkta
, ja eksistē tāda punkta
 apkārtne, ka
apkārtne, ka
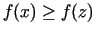 visiem
visiem 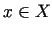 no šīs apkārtnes.
Ja pie tam
no šīs apkārtnes.
Ja pie tam 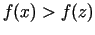 , kad
, kad 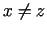 , tad saka, ka minimums ir
stingrs.
, tad saka, ka minimums ir
stingrs.
-
1.3. piezīme.
- Funkcijai var būt vairāki (un pat bezgalīgi daudz)
lokālo minimumu (skat. 1.2. zīm.).
Saka, ka kopā
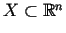 definētai
funkcijai
definētai
funkcijai
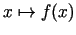 ir globāls minimums punktā
ir globāls minimums punktā
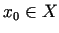 , ja
, ja
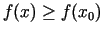 visiem
visiem  no kopas
no kopas 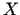 .
.
Analoģiski var definēt funkcijas lokālo maksimumu un globālo
maksimumu.
Par funkcijas ekstrēmu
sauc jebkuru šīs funkcijas maksimumu vai minimumu (lokālo un
globālo) .
Literatūrā bieži vien aplūko tikai
minimuma gadījumu, jo funkcijas 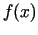 maksimuma atrašanas
problēma
maksimuma atrašanas
problēma
ir ekvivalenta funkcijas 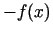 minimuma atrašanas problēmai
minimuma atrašanas problēmai
Piemēram, kopā
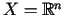 definētai funkcijai
definētai funkcijai
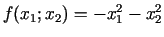 punkts
punkts 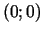 ir globālā maksimuma punkts, bet šajā kopā
definētai funkcijai
ir globālā maksimuma punkts, bet šajā kopā
definētai funkcijai
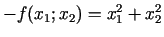 punkts
punkts 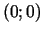 ir globālā minimuma punkts.
ir globālā minimuma punkts.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.1.3. Ekstrēma eksistences nepieciešamie nosacījumi
Augstāk: 1.1. Brīvais ekstrēms
Iepriekšējais: 1.1.1. Problēma par peļņas maksimumu
2002-05-04
![]() sauc attēlojumu, kurā katram
elementam
sauc attēlojumu, kurā katram
elementam ![]() atbilst pilnīgi noteikts elements
atbilst pilnīgi noteikts elements ![]() ,
kuru apzīmē ar
,
kuru apzīmē ar ![]() un sauc par elementa
un sauc par elementa ![]() attēlu
attēlojumā
attēlu
attēlojumā ![]() . Speciālgadījumā
. Speciālgadījumā ![]() un
un ![]() var būt viena un tā
pati kopa. Aktuāls ir gadījums, kad kopa
var būt viena un tā
pati kopa. Aktuāls ir gadījums, kad kopa ![]() ir vienāda ar Eiklīda
telpu
ir vienāda ar Eiklīda
telpu
![]() vai kādu tās apakškopu, bet kopa
vai kādu tās apakškopu, bet kopa ![]() ir
vienāda ar reālo skaitļu kopu
ir
vienāda ar reālo skaitļu kopu
![]() .
.
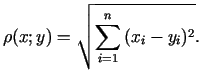
![]() un
rādiusu
un
rādiusu ![]() sauc telpas
sauc telpas
![]() apakškopu
apakškopu
![]() , kas sastāv no visiem tiem un tikai tiem punktiem
, kas sastāv no visiem tiem un tikai tiem punktiem
![]() , kuru attālums
, kuru attālums ![]() līdz punktam
līdz punktam ![]() ir
mazāks nekā skaitlis
ir
mazāks nekā skaitlis ![]() , t.i.,
, t.i.,
![\includegraphics[width=12cm]{C:/TEXfiles/felikss/1n1z.eps}](img52.gif)
![]() sauc par vaļēju kopu, ja
jebkurš tās punkts ir iekšējais.
sauc par vaļēju kopu, ja
jebkurš tās punkts ir iekšējais.
![]() definētai funkcijai
definētai funkcijai ![]() ir
lokāls minimums punktā
ir
lokāls minimums punktā ![]() , ja eksistē tāda punkta
, ja eksistē tāda punkta
![]() apkārtne, ka
apkārtne, ka
![]() visiem
visiem ![]() no šīs apkārtnes.
Ja pie tam
no šīs apkārtnes.
Ja pie tam ![]() , kad
, kad ![]() , tad saka, ka minimums ir
stingrs.
, tad saka, ka minimums ir
stingrs.
![\includegraphics[width=13cm]{C:/TEXfiles/felikss/1n2z.eps}](img63.gif)
![]() definētai
funkcijai
definētai
funkcijai
![]() ir globāls minimums punktā
ir globāls minimums punktā
![]() , ja
, ja
![]() visiem
visiem ![]() no kopas
no kopas ![]() .
.