


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.1.2. Definīcijas
Augstāk: 1.1. Brīvais ekstrēms
Iepriekšējais: 1.1. Brīvais ekstrēms
Problēma par peļņas maksimumu. Monopolists (kurš pats
nosaka cenas) pārdod preces divos tirgos. Nedēļas laikā pirmajā
tirgū pārdotās preces daudzuma 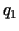 (tūkst. gab.) atkarību no
preces cenas
(tūkst. gab.) atkarību no
preces cenas 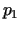 var izteikt kā
var izteikt kā
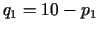 (- tā saucamā
pieprasījuma funkcija). Savukārt otrajā tirgū
(- tā saucamā
pieprasījuma funkcija). Savukārt otrajā tirgū
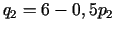 . Izdevumu
. Izdevumu 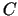 atkarību no pārdotās preces
daudzuma var izteikt ar formulu
atkarību no pārdotās preces
daudzuma var izteikt ar formulu
Jautājums. Kādām daudzumu 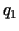 un
un 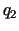 vērtībām (un
pie kādām cenām
vērtībām (un
pie kādām cenām 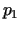 un
un 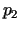 ) ienākums
) ienākums 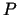 būs
maksimāls?
būs
maksimāls?
Problēmas formalizēšana.
Vai vispār eksistē cenas, pie kurām ienākums
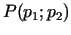 ir
maksimāls, un, ja eksistē, kā tās noteikt? Izteiksim cenas
ir
maksimāls, un, ja eksistē, kā tās noteikt? Izteiksim cenas 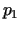 un
un 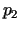 ar preču daudzumiem
ar preču daudzumiem 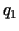 un
un 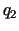 :
:
un izteiksim 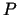 kā argumentu
kā argumentu 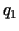 un
un 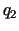 funkciju:
funkciju:
Tātad ekonomiskā problēma reducējas uz divu argumentu funkcijas
maksimuma atrašanas problēmu. Dotās problēmas risinājums tiks dots
punktā 1.1.6., bet tagad apskatīsim paņēmienus, ar kuru
palīdzību var atrast vairāku argumentu funkciju ekstrēmus,
protams, ja tādi eksistē.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.1.2. Definīcijas
Augstāk: 1.1. Brīvais ekstrēms
Iepriekšējais: 1.1. Brīvais ekstrēms
2002-05-04
![]() (tūkst. gab.) atkarību no
preces cenas
(tūkst. gab.) atkarību no
preces cenas ![]() var izteikt kā
var izteikt kā
![]() (- tā saucamā
pieprasījuma funkcija). Savukārt otrajā tirgū
(- tā saucamā
pieprasījuma funkcija). Savukārt otrajā tirgū
![]() . Izdevumu
. Izdevumu ![]() atkarību no pārdotās preces
daudzuma var izteikt ar formulu
atkarību no pārdotās preces
daudzuma var izteikt ar formulu
![]() un
un ![]() vērtībām (un
pie kādām cenām
vērtībām (un
pie kādām cenām ![]() un
un ![]() ) ienākums
) ienākums ![]() būs
maksimāls?
būs
maksimāls?