


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4.5. Jautājumi
Augstāk: 4. KVADRĒJAMĪBAS KRITĒRIJI
Iepriekšējais: 4.3.2. Līklīnijas sektora kvadrējamība un tās
-
4.3. teorēma.
- [Laukuma aditivitāte]
Ja 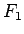 ,
, 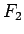 ir kvadrējamas plaknes figūras, kurām nav kopīgu
iekšējo punktu un
ir kvadrējamas plaknes figūras, kurām nav kopīgu
iekšējo punktu un
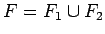 , tad
, tad  ir kvadrējama figūra, pie
tam
ir kvadrējama figūra, pie
tam
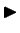 Tā kā
Tā kā 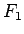 un
un 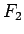 ir kvadrējamas plaknes
figūras, tad jebkuram
ir kvadrējamas plaknes
figūras, tad jebkuram
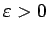 eksistē tādi planes
daudzstūri
eksistē tādi planes
daudzstūri 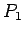 ,
, 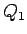 un
un 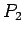 ,
, 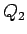 (
(
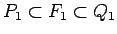 ;
;
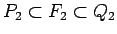 ), ka
), ka
Apskata plaknes daudzstūrus
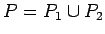 ,
,
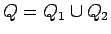 .
Acīmredzami,
.
Acīmredzami,
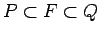 .
.
Plaknes daudzstūriem 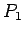 un
un 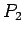 nav kopīgu iekšējo punktu, tāpēc
nav kopīgu iekšējo punktu, tāpēc
Plaknes daudzstūriem 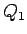 un
un 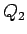 var būt arī kopīgi iekšējie
punkti, tāpēc
var būt arī kopīgi iekšējie
punkti, tāpēc
Apskata
Saskaņā ar kvadrējamības 1. kritēriju (skat. 4.1. teorēmu)
 ir kvadrējama figūra, pie tam
ir kvadrējama figūra, pie tam
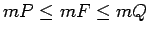 .
.
Tādējādi
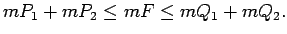 |
(4.3) |
No sakarībām
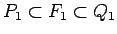 ;
;
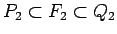 seko, ka
seko, ka
Saskaitot šīs nevienādības iegūst, ka
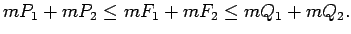 |
(4.4) |
No nevienādībām (4.3) un (4.4) seko, ka divas
konstantes 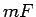 un
un
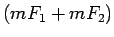 ir iekļautas starp lielumiem
ir iekļautas starp lielumiem
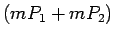 un
un
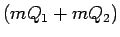 , kuri var kļūt pēc patikas tuvi, tāpēc
, kuri var kļūt pēc patikas tuvi, tāpēc
-
4.1. piezīme.
-

- No plaknes daudzstūra laukuma invariances (vai monotonitātes)
un plaknes figūras laukuma definīcijas izriet plaknes figūras
laukuma invariance (vai monotonitāte).
- Divu plaknes kvadrējamu figūru starpība
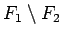 un
šķēlums
un
šķēlums
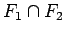 ir kvadrējamas figūras.
ir kvadrējamas figūras.
- Ar matemātiskās indukcijas metodi laukuma aditivitātes
īpašību var vispārināt attiecībā uz jebkura galīga skaita
kvadrējamu figūru, kurām nav kopīgu iekšējo punktu, apvienojumu.
- Analogi var definēt kubējamu telpas ķermeni
 , tā tilpumu
, tā tilpumu
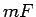 , formulēt un pierādīt kubējamības kritērijus un tilpuma
īpašības.
, formulēt un pierādīt kubējamības kritērijus un tilpuma
īpašības.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4.5. Jautājumi
Augstāk: 4. KVADRĒJAMĪBAS KRITĒRIJI
Iepriekšējais: 4.3.2. Līklīnijas sektora kvadrējamība un tās
2002-11-06
![]() Tā kā
Tā kā ![]() un
un ![]() ir kvadrējamas plaknes
figūras, tad jebkuram
ir kvadrējamas plaknes
figūras, tad jebkuram
![]() eksistē tādi planes
daudzstūri
eksistē tādi planes
daudzstūri ![]() ,
, ![]() un
un ![]() ,
, ![]() (
(
![]() ;
;
![]() ), ka
), ka
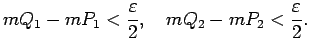
![]() ,
,
![]() .
Acīmredzami,
.
Acīmredzami,
![]() .
.
![]() un
un ![]() var būt arī kopīgi iekšējie
punkti, tāpēc
var būt arī kopīgi iekšējie
punkti, tāpēc
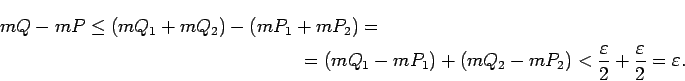
![]() ir kvadrējama figūra, pie tam
ir kvadrējama figūra, pie tam
![]() .
.
![]() ;
;
![]() seko, ka
seko, ka
![]() un
un
![]() ir iekļautas starp lielumiem
ir iekļautas starp lielumiem
![]() un
un
![]() , kuri var kļūt pēc patikas tuvi, tāpēc
, kuri var kļūt pēc patikas tuvi, tāpēc