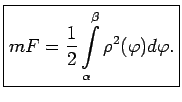Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4.4. Plaknes figūras laukuma īpašības
Augstāk: 4.3. Kvadrējamu figūru piemēri
Iepriekšējais: 4.3.1. Līklīnijas trapeces kvadrējamība un tās
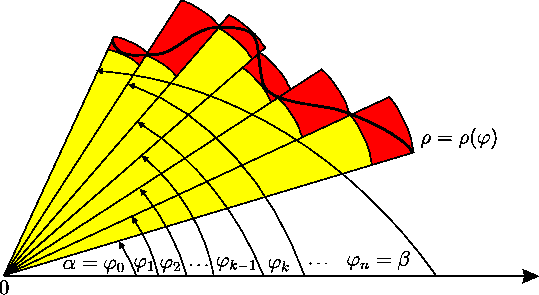
Polārajā koordinātu sistēmā apskata plaknes figūru  , kuru
ierobežo divi stari
, kuru
ierobežo divi stari
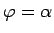 ,
,
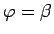 un intervālā
nepārtrauktas un nenegatīvas funkcijas
un intervālā
nepārtrauktas un nenegatīvas funkcijas
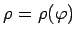 grafiks
(4.3. zīm.).
grafiks
(4.3. zīm.).
Šādu plaknes figūru sauc par līklīnijas sektoru.
Lai pierādītu līklīnijas sektora kvadrējamību un aprēķinātu tā
laukumu, rīkojas šādi:
- izveido intervāla
![$ [\alpha;\beta]$](img988.gif) sasmalcinājumu
sasmalcinājumu
- apzīmē ar
 .
.
Līklīnijas sektorā  ievelk kvadrējamu plaknes figūru
ievelk kvadrējamu plaknes figūru 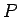 , kas
sastāv no tādiem riņķa sektoriem, kuriem centra leņķi ir
, kas
sastāv no tādiem riņķa sektoriem, kuriem centra leņķi ir
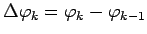 un rādiusi atbilstoši
un rādiusi atbilstoši
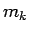 .
.
Analogi ap  apvelk kvadrējamu plaknes figūru
apvelk kvadrējamu plaknes figūru 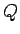 (šoreiz riņķa
sektoru rādiusi ir
(šoreiz riņķa
sektoru rādiusi ir 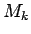 ).
).
Aprēķina 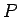 un
un 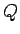 laukumus:
laukumus:
Skaitļus 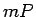 un
un 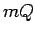 var uzskatīt par funkcijas
var uzskatīt par funkcijas
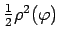 Darbū summām, kas atbilst izveidotajam
intervāla
Darbū summām, kas atbilst izveidotajam
intervāla
![$ [\alpha;\beta]$](img988.gif) sasmalcinājumam. Tādējādi
sasmalcinājumam. Tādējādi
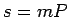 un
un
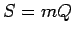 .
.
Tā kā funkcija
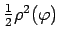 nepārtraukta intervālā
nepārtraukta intervālā
![$ [\alpha;\beta]$](img988.gif) , tad tā ir integrējama šajā intervālā un saskaņā
ar integrējamības kritēriju jebkuram
, tad tā ir integrējama šajā intervālā un saskaņā
ar integrējamības kritēriju jebkuram
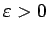 eksistē tāds
eksistē tāds
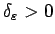 , ka visiem intervāla
, ka visiem intervāla
![$ [\alpha;\beta]$](img988.gif) sasmalcinājumiem ar soli
sasmalcinājumiem ar soli
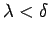 izpildās nevienādība
izpildās nevienādība
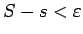 . Tādējādi eksistē tādas kvadrējamas plaknes
figūras
. Tādējādi eksistē tādas kvadrējamas plaknes
figūras 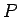 un
un 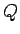
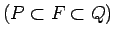 , ka
, ka
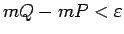 . Saskaņā ar kvadrējamības 2. kritēriju (skat.
4.2. teorēmu)
. Saskaņā ar kvadrējamības 2. kritēriju (skat.
4.2. teorēmu)  ir kvadrējama figūra.
ir kvadrējama figūra.
Apzīmē integrāli
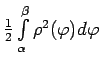 ar
ar
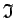 un līklīnijas sektora laukumu ar
un līklīnijas sektora laukumu ar 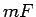 . Tā kā divas
konstantes
. Tā kā divas
konstantes
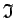 un
un 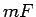 ir iekļautas starp
ir iekļautas starp 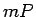 un
un 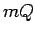 ,
kuri var kļūt pēc patikas tuvi, tad
,
kuri var kļūt pēc patikas tuvi, tad
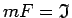 jeb
jeb



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4.4. Plaknes figūras laukuma īpašības
Augstāk: 4.3. Kvadrējamu figūru piemēri
Iepriekšējais: 4.3.1. Līklīnijas trapeces kvadrējamība un tās
2002-11-06
![$\displaystyle M_k=\sup\limits_{[\varphi_{k-1};\varphi_k]}\rho(\varphi)=
\max\limits_{[\varphi_{k-1};\varphi_k]}\rho(\varphi)\/,$](img991.gif)
![]() ievelk kvadrējamu plaknes figūru
ievelk kvadrējamu plaknes figūru ![]() , kas
sastāv no tādiem riņķa sektoriem, kuriem centra leņķi ir
, kas
sastāv no tādiem riņķa sektoriem, kuriem centra leņķi ir
![]() un rādiusi atbilstoši
un rādiusi atbilstoši
![]() .
.
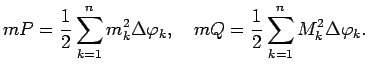
![]() un
un ![]() var uzskatīt par funkcijas
var uzskatīt par funkcijas
![]() Darbū summām, kas atbilst izveidotajam
intervāla
Darbū summām, kas atbilst izveidotajam
intervāla
![]() sasmalcinājumam. Tādējādi
sasmalcinājumam. Tādējādi
![]() un
un
![]() .
.
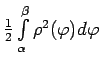 ar
ar