


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4. PARAMETRISKI UZDOTAS FUNKCIJAS UN VEKTORFUNKCIJAS
Augstāk: 3. ATVASINĀJUMA LIETOJUMI FUNKCIJU PĒTĪŠANĀ
Iepriekšējais: 3.10. Jautājumi
- Pierādīt 3.1. teorēmas sekas.
- Pierādīt, ka
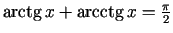 .
.
- Formulēt un pierādīt intervālā dilstošas funkcijas nepieciešamo nosacījumu.
- Formulēt un pierādīt intervālā dilstošas funkcijas pietiekamo nosacījumu.
- Lai intervālā
 diferencējama funkcija
diferencējama funkcija  būtu nedilstoša šajā intervālā, ir nepieciešami un pietiekami, lai
visiem
būtu nedilstoša šajā intervālā, ir nepieciešami un pietiekami, lai
visiem 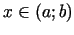 izpildītos
izpildītos
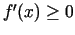 . Pierādīt to!
. Pierādīt to!
- Atrast šādu funkciju monotonitātes intervālus:
-
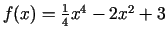 ;
;
-
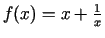 ;
;
-
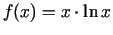 ;
;
-
![$ f(x)=\sqrt[3]{x^2}$](img902.gif) .
.
- Pierādīt 3.4. teorēmu minimuma punkta
gadījumā.
- Pierādīt 3.5. teorēmu gadījumam, kad, argumentam ejot caur
 , atvasinājums maina zīmi no
, atvasinājums maina zīmi no 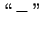 uz
uz 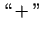 .
.
- Pierādīt 3.6. teorēmu gadījumam,
kad
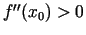 .
.
- Atrast šādu funkciju ekstrēmus (izmantot gan
pirmo, gan otro ekstrēmu noteikšanas kārtulu):
-
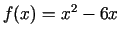 ;
;
-
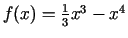 ;
;
-
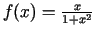 ;
;
-
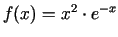 .
.
- Atrast šādu funkciju vismazāko un vislielāko
vērtību norādītajā intervālā:
-
![$ f(x)=x^4-8x^2-9,\quad [-1;1]$](img907.gif) ;
;
-
![$ f(x)=x^4-8x^2-9,\quad [0;3]$](img908.gif) ;
;
-
![$ f(x)=x^3-1,5x^2-6x+1,\quad [-2;0]$](img909.gif) ;
;
-
![$ f(x)=x+\sqrt{x},\quad [0;4]$](img910.gif) .
.
- Pierādīt, ka no visiem taisnleņķa
trijstūriem, kuriem ir dotā garuma hipotenūza, vislielākais
laukums ir vienādsānu trijstūrim.
- Doto pozitīvo skaitli izteikt kā divu saskaitāmo
summu, kuru reizinājums ir vislielākais.
- Taisnstūra paralēlskaldņa vaļējas
tvertnes tilpumam jābūt
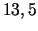 l. Kā ir jāizvēlas tvertnes
lineārie izmēri, lai tās pagatavošanai tiktu izlietots vismazāk
materiāla?
l. Kā ir jāizvēlas tvertnes
lineārie izmēri, lai tās pagatavošanai tiktu izlietots vismazāk
materiāla?
- Formulēt un pierādīt funkcijas grafika izliekuma
pietiekamo nosacījumu.
- Atrast šādu funkciju grafiku izliekuma un ieliekuma
intervālus:
-
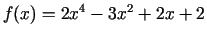 ;
;
-
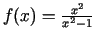 ;
;
-
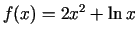 ;
;
-
![$ f(x)=\sqrt[3]{x}$](img77.gif) .
.
- Pierādīt 3.8. teorēmu.
- Atrast šādu funkciju grafiku pārliekuma punktus:
-
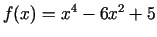 ;
;
-
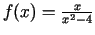 ;
;
-
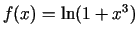 ;
;
-
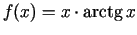 .
.
- Atrast šādu funkciju grafiku asimptotas:
-
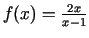 ;
;
-
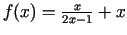 ;
;
-
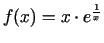 ;
;
-
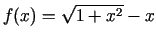 .
.
- Izpētīt šādas funkcijas un uzzīmēt
to grafikus:
-
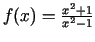 ;
;
-
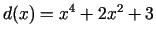 ;
;
-
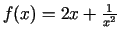 ;
;
-
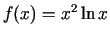 ;
;
-
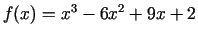 ;
;
-
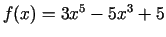 ;
;
-
![$ f(x)=x-3\sqrt[3]{x}$](img682.gif) .
.
- Pierādīt nevienādības, pētot funkciju
monotonitāti ar atvasinājumu palīdzību:
-
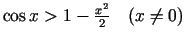 ;
;
-
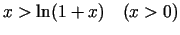 ;
;
-
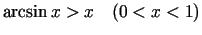 ;
;
-
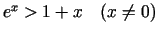 .
.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4. PARAMETRISKI UZDOTAS FUNKCIJAS UN VEKTORFUNKCIJAS
Augstāk: 3. ATVASINĀJUMA LIETOJUMI FUNKCIJU PĒTĪŠANĀ
Iepriekšējais: 3.10. Jautājumi
2002-01-21
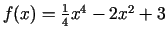 ;
;
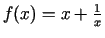 ;
;
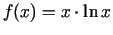 ;
;
![$ f(x)=\sqrt[3]{x^2}$](img902.gif) .
.
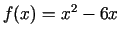 ;
;
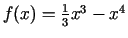 ;
;
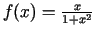 ;
;
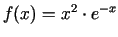 .
.
![$ f(x)=x^4-8x^2-9,\quad [-1;1]$](img907.gif) ;
;
![$ f(x)=x^4-8x^2-9,\quad [0;3]$](img908.gif) ;
;
![$ f(x)=x^3-1,5x^2-6x+1,\quad [-2;0]$](img909.gif) ;
;
![$ f(x)=x+\sqrt{x},\quad [0;4]$](img910.gif) .
.
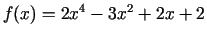 ;
;
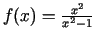 ;
;
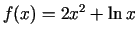 ;
;
![$ f(x)=\sqrt[3]{x}$](img77.gif) .
.
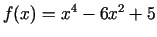 ;
;
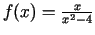 ;
;
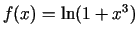 ;
;
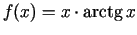 .
.
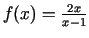 ;
;
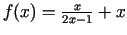 ;
;
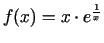 ;
;
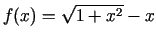 .
.
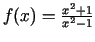 ;
;
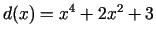 ;
;
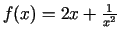 ;
;
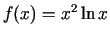 ;
;
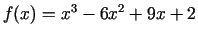 ;
;
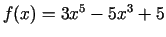 ;
;
![$ f(x)=x-3\sqrt[3]{x}$](img682.gif) .
.
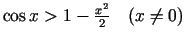 ;
;
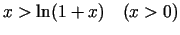 ;
;
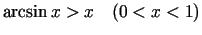 ;
;
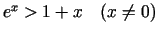 .
.