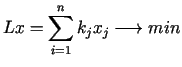Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.3.2. Simpleksa metodes algoritms
Augstāk: 3.3. Simpleksa metode
Iepriekšējais: 3.3. Simpleksa metode
Saskaņā ar iepriekšējā nodaļā teikto lineārās programmēšanas
problēmas atrisinājums (divu dimensiju gadījumā) vienmēr atrodas
vienā no pieļaujamā apgabala virsotnēm. Analoģisks rezultāts
ir spēkā arī vispārīgā gadījumā. Aplūkosim minimizācijas problēmu
mērķa funkcijai
ar 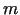 ierobežojumiem (3.7), kurus pierakstīsim matricu
formā:
ierobežojumiem (3.7), kurus pierakstīsim matricu
formā:
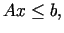 |
(3.10) |
kur 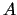 ir
ir 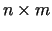 matrica,
matrica,
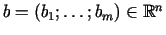 . Pieļaujamais apgabals
. Pieļaujamais apgabals
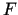 , kuru nosaka nevienādība (3.10), ir izliekts
daudzskaldnis telpā
, kuru nosaka nevienādība (3.10), ir izliekts
daudzskaldnis telpā
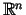 .
.
Pierādīsim, ka kopa
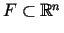 ir izliekta, t.i., kopa
ir izliekta, t.i., kopa
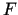 reizē ar jebkuriem diviem saviem punktiem
reizē ar jebkuriem diviem saviem punktiem  un
un 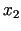 satur arī nogriezni ar galapunktiem
satur arī nogriezni ar galapunktiem  un
un 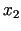 :
:
![$\displaystyle [x_1;x_2]=\{x\in\mathbb{R}^{n}:\;{\alpha}x_{1}+(1-\alpha)x_{2}, 0\leq\alpha\leq 1\}.$](img948.gif) |
(3.11) |
Tiešām, ja
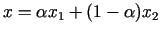 , kur
, kur
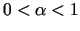 , tad
, tad
un, tā kā apgabals 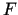 ir definēts ar nevienādību (3.10),
tad visi nogriežņa (3.11) punkti pieder kopai
ir definēts ar nevienādību (3.10),
tad visi nogriežņa (3.11) punkti pieder kopai
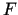 .
.
Viegli redzēt, ka kopas 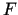 robeža
sastāv no hiperplakņu
robeža
sastāv no hiperplakņu
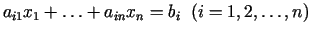 |
(3.12) |
segmentiem.
Par 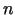 -dimensionāla daudzskaldņa
-dimensionāla daudzskaldņa
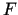 virsotnēm sauc punktus, kuri pieder vismaz
virsotnēm sauc punktus, kuri pieder vismaz 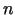 hiperplaknēm (3.12).
hiperplaknēm (3.12).
Triju (vai
divu) dimensiju gadījumā, t.i., ja 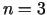 (vai
(vai 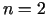 ), var
sniegt uzskatāmu daudzskaldņa ģeometrisko interpretāciju. Ja
), var
sniegt uzskatāmu daudzskaldņa ģeometrisko interpretāciju. Ja 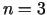 , tad
, tad 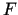 ir daudzskaldnis, un vismaz triju plakņu, kuras veido
ir daudzskaldnis, un vismaz triju plakņu, kuras veido
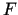 robežu, kopējais punkts ir daudzskaldņa
robežu, kopējais punkts ir daudzskaldņa 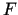 virsotne. Tā,
piemēram, 3.2. zīmējumā attēlotā kopa
virsotne. Tā,
piemēram, 3.2. zīmējumā attēlotā kopa 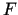 - vienības kubs ar
nošķeltu virsotni - izliekts daudzskaldnis ar
- vienības kubs ar
nošķeltu virsotni - izliekts daudzskaldnis ar 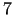 skaldnēm un
skaldnēm un 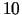 virsotnēm. Katra
virsotnēm. Katra 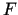 virsotne ir triju plakņu, kuras veido
virsotne ir triju plakņu, kuras veido 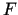 robežu, kopīgais punkts. Protams, var iedomāties daudzskaldni
(
robežu, kopīgais punkts. Protams, var iedomāties daudzskaldni
(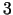 -dimensiju telpā) ar virsotni, kura ir vairāk nekā triju
plakņu kopīgais punkts, piemēram, piramīdu, kuras pamatā ir
četrstūris.
-dimensiju telpā) ar virsotni, kura ir vairāk nekā triju
plakņu kopīgais punkts, piemēram, piramīdu, kuras pamatā ir
četrstūris.
Lineārās programmēšanas
teorijas pamatrezultāts saka, ka, ja lineārās programmēšanas
problēmai ir atrisinājums, tad obligāti atradīsies šīs
problēmas pieļaujamā apgabala 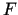 virsotne, kas sakrīt ar šo
atrisinājumu.
virsotne, kas sakrīt ar šo
atrisinājumu.
Šim faktam var sniegt
uzskatāmu ģeometrisko interpretāciju, apskatot lineārās
programmēšanas problēmas divu un triju dimensiju gadījumā. Tiešām,
iedomāsimies 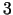 -dimensionālu izliektu daudzskaldni (- pieļaujamais apgabals
-dimensionālu izliektu daudzskaldni (- pieļaujamais apgabals 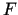 ), kuru šķeļ plakne (- mērķa funkcijas
līmeņvirsma). Paralēli pārnesot šo plakni, tā "pēdējā momentā"
pieskaras apgabala
), kuru šķeļ plakne (- mērķa funkcijas
līmeņvirsma). Paralēli pārnesot šo plakni, tā "pēdējā momentā"
pieskaras apgabala 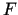 robežai. Šis "moments", precīzāk sakot,
pieskaršanās punkta koordinātas, atbilst ekstremālās problēmas
atrisinājumam. Pārvietojot līmeņvirsmu (plakni) vienā virzienā,
iegūstam minimizācijas problēmas atrisinājumu, bet,
pārvietojot to pretējā virzienā, iegūstam maksimizācijas
problēmas atrisinājumu. Mērķa funkcijas līmeņvirsmas
pieskaršanās pieļaujamajam apgabalam
var notikt šādi:
robežai. Šis "moments", precīzāk sakot,
pieskaršanās punkta koordinātas, atbilst ekstremālās problēmas
atrisinājumam. Pārvietojot līmeņvirsmu (plakni) vienā virzienā,
iegūstam minimizācijas problēmas atrisinājumu, bet,
pārvietojot to pretējā virzienā, iegūstam maksimizācijas
problēmas atrisinājumu. Mērķa funkcijas līmeņvirsmas
pieskaršanās pieļaujamajam apgabalam
var notikt šādi:
- līmeņvirsma pieskaras pieļaujamā apgabala virsotnei,
- līmeņvirsma pieskaras pieļaujamā apgabala šķautnei,
- līmeņvirsma pieskaras pieļaujamā apgabala skaldnei.
Otrajā un trešajā gadījumā ekstrēmu problēmai ir bezgalīgi daudz
atrisinājumu, taču starp tiem noteikti ir arī pieļaujamā
apgabala virsotnes.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.3.2. Simpleksa metodes algoritms
Augstāk: 3.3. Simpleksa metode
Iepriekšējais: 3.3. Simpleksa metode
2002-05-04