Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.2.2 Minimuma gadījums
Augstāk: 3.2. Lineārās programēšanas uzdevumu risināšanas grafiskā
Iepriekšējais: 3.2. Lineārās programēšanas uzdevumu risināšanas grafiskā
Meģināsim analizēt lineārās programmēšanas uzdevuma
ģeometrisko saturu. Nevienādības (3.7) definē
daudzskaldņa tipa apgabalu 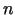 -dimensiju telpā
-dimensiju telpā
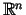 .
Tiešam, pirmā no nevienādībam (3.7) definē telpas
.
Tiešam, pirmā no nevienādībam (3.7) definē telpas
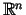 pustelpu, kura atrodas vienā pusē attiecībā pret
hiperplakni
pustelpu, kura atrodas vienā pusē attiecībā pret
hiperplakni
Apzīmēsim šo hiperplakni ar 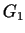 . Otrā no nevienādībam
(3.7) definē pustelpu
. Otrā no nevienādībam
(3.7) definē pustelpu 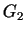 utt. Rezultātā iegūstam
telpisku figūru
utt. Rezultātā iegūstam
telpisku figūru
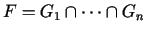 , kura veido
daudzskaldni telpā
, kura veido
daudzskaldni telpā
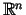 . Šī daudzskaldņa robeža sastāv
no hiperplakņu
. Šī daudzskaldņa robeža sastāv
no hiperplakņu
segmentiem. Kopu 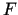 sauc par pieļaujamo apgabalu, jo par
lineārās programmēšanas uzdevuma atrisinājumu var būt tikai punkts
sauc par pieļaujamo apgabalu, jo par
lineārās programmēšanas uzdevuma atrisinājumu var būt tikai punkts
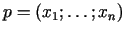 , kurš pieder kopai
, kurš pieder kopai
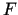 .
.
Piemēram, 1. problēmā kopas G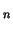 ir
šādas:
ir
šādas:
Katra no šīm kopām ir
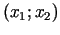 -plaknes pusplakne.
Pieļaujamais apgabals
-plaknes pusplakne.
Pieļaujamais apgabals
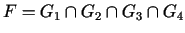 ir
daudzstūris
ir
daudzstūris 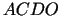 (skat. 3.1. zīm.).
(skat. 3.1. zīm.).
3. problēma. Sniegsim vēl vienu pieļaujamā apgabala
piemēru. Aplūkosim problēmu 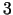 -dimensiju telpā
-dimensiju telpā
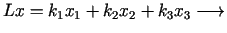 ekstrēms ekstrēms |
|
ar 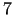 ierobežojumiem nevienādību veidā:
ierobežojumiem nevienādību veidā:
Katra no šīm nevienādībām definē pustelpu 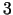 -dimensiju Eiklīda
telpā
-dimensiju Eiklīda
telpā
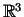 . Šo
. Šo 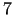 pustelpu kopējā daļa ir vienības
kubs bez virsotnes (skat. 3.2. zīm.).
pustelpu kopējā daļa ir vienības
kubs bez virsotnes (skat. 3.2. zīm.).
Gadījumā, kad telpas dimensiju skaits lielāks nekā
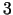 , izpildīt
, izpildīt 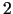 -dimensionālu zīmējumu ir sarežģīti, un
tas nebūtu informatīvs (pamēģiniet izveidot
-dimensionālu zīmējumu ir sarežģīti, un
tas nebūtu informatīvs (pamēģiniet izveidot
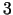 -dimensionāla kuba
-dimensionāla kuba 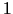 -dimensionālu zīmējumu).Tāpēc
lineārās programmēšanas uzdevuma risināšanas grafiskā
metode pārsvarā tiek lietota, risinot uzdevumus
-dimensionālu zīmējumu).Tāpēc
lineārās programmēšanas uzdevuma risināšanas grafiskā
metode pārsvarā tiek lietota, risinot uzdevumus 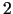 vai
vai 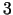 dimensiju gadījumā.
dimensiju gadījumā.
Grafiskās metodes lietošanas shēma ir šāda. Tiek attēlots
pieļaujamais apgabals 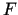 , kuru veido daudzstūris
, kuru veido daudzstūris 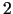 dimensiju gadījumā, un daudzskaldnis
dimensiju gadījumā, un daudzskaldnis 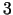 dimensiju gadījumā. Tiek
attēlota mērķa funkcijas līmeņlīniju kopa
dimensiju gadījumā. Tiek
attēlota mērķa funkcijas līmeņlīniju kopa 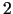 dimensiju gadījumā un līmeņvirsmu kopa
dimensiju gadījumā un līmeņvirsmu kopa 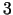 dimensiju
gadījumā, t.i., punktu
dimensiju
gadījumā, t.i., punktu
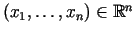 ,
kuriem
,
kuriem
kopa, ja 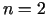 vai
vai 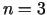 . Ja kāda līmeņlīnija (vai attiecīgi
līmeņvirsma) dotajam
. Ja kāda līmeņlīnija (vai attiecīgi
līmeņvirsma) dotajam 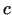 ir konstruēta, tad pārējās līmeņlīnijas
(vai attiecīgi līmeņvirsmas) iegūst no dotās ar paralēlās pārneses
palīdzību. Mainot
ir konstruēta, tad pārējās līmeņlīnijas
(vai attiecīgi līmeņvirsmas) iegūst no dotās ar paralēlās pārneses
palīdzību. Mainot 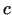 , nosaka mērķa funkcijas vērtību
palielināšanās virzienu (ja ir jāatrod mērķa funkcijas maksimums)
vai mērķa funkcijas vērtību samazināšanās virziens (ja ir jāatrod
mērķa funkcijas minimums). Visbeidzot, maksimuma problēmas
gadījumā nosaka maksimālo parametra
, nosaka mērķa funkcijas vērtību
palielināšanās virzienu (ja ir jāatrod mērķa funkcijas maksimums)
vai mērķa funkcijas vērtību samazināšanās virziens (ja ir jāatrod
mērķa funkcijas minimums). Visbeidzot, maksimuma problēmas
gadījumā nosaka maksimālo parametra 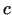 vērtību
vērtību 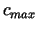 , pie
kuras līmeņlīnijai (vai attiecīgi līmeņvirsmai) ir kopīgs punkts
ar pieļaujamo apgabalu. Šī kopīgā punkta koordinātas arī ir
apskatāmās maksimuma problēmas atrisinājums. Ievietojot atrastās
koordinātas mērķa funkcijas izteiksmē, iegūst tās maksimālo
vērtību pie dotajiem ierobežojumiem. Minimuma problēmas
gadījumā nosaka minimālo parametra
, pie
kuras līmeņlīnijai (vai attiecīgi līmeņvirsmai) ir kopīgs punkts
ar pieļaujamo apgabalu. Šī kopīgā punkta koordinātas arī ir
apskatāmās maksimuma problēmas atrisinājums. Ievietojot atrastās
koordinātas mērķa funkcijas izteiksmē, iegūst tās maksimālo
vērtību pie dotajiem ierobežojumiem. Minimuma problēmas
gadījumā nosaka minimālo parametra 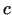 vērtību
vērtību  ,
pie kuras līmeņlīnijai (vai attiecīgi līmeņvirsmai) ir kopīgs
punkts ar pieļaujamo apgabalu. Šī kopīgā punkta koordinātas arī ir
apskatāmās minimuma problēmas atrisinājums. Ievietojot atrastās
koordinātas mērķa funkcijas izteiksmē, iegūst tās minimālo
vērtību pie dotajiem ierobežojumiem.
,
pie kuras līmeņlīnijai (vai attiecīgi līmeņvirsmai) ir kopīgs
punkts ar pieļaujamo apgabalu. Šī kopīgā punkta koordinātas arī ir
apskatāmās minimuma problēmas atrisinājums. Ievietojot atrastās
koordinātas mērķa funkcijas izteiksmē, iegūst tās minimālo
vērtību pie dotajiem ierobežojumiem.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.2.2 Minimuma gadījums
Augstāk: 3.2. Lineārās programēšanas uzdevumu risināšanas grafiskā
Iepriekšējais: 3.2. Lineārās programēšanas uzdevumu risināšanas grafiskā
2002-05-04
![]() -dimensiju telpā
-dimensiju telpā
![]() .
Tiešam, pirmā no nevienādībam (3.7) definē telpas
.
Tiešam, pirmā no nevienādībam (3.7) definē telpas
![]() pustelpu, kura atrodas vienā pusē attiecībā pret
hiperplakni
pustelpu, kura atrodas vienā pusē attiecībā pret
hiperplakni