Naftas no avota A cena par vienu tonnu ir $
Atrisināsim grafiski šādu problēmu.
Problēma par optimālu pirkšanas plānu. Kādas valsts pieprasījums pēc naftas produktiem (miljonos tonnu) ir šāds:
|
Tiek sastādīts šķidrās naftas pirkšanas plāns nākamajam gadam.
Naftu iepērk no diviem atsevišķiem avotiem (apzīmēsim tos ar A un
B). Naftas A un B sastāvs (procentos) ir
šāds.
|
Naftas no avota A cena par vienu tonnu ir $ ![]() , bet naftas
no avota B cena par tonnu - $
, bet naftas
no avota B cena par tonnu - $ ![]() . Cik jānopērk naftas no
abiem avotiem, lai nodrošinātu valsti ar nepieciešamo degvielas
daudzumu un samaksa par šķidro naftu būtu
minimālā?
. Cik jānopērk naftas no
abiem avotiem, lai nodrošinātu valsti ar nepieciešamo degvielas
daudzumu un samaksa par šķidro naftu būtu
minimālā?
Atrisinājums. Formalizēsim doto problēmu.
Apzīmēsim:
Pirkšanas ierobežojumi:
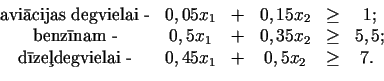 |
Mērķa funkcija - pirktās naftas cena:
Tātad matemātiski doto problēmu var formulēt šādi:
Nav būtiski, ka nevienādībās (3.9) figurē zīme ![]() . Ja
nevienādību (3.9) abas puses pareizinātu ar
``-1'', tad šīs nevienādības būtu formā
(3.7).
. Ja
nevienādību (3.9) abas puses pareizinātu ar
``-1'', tad šīs nevienādības būtu formā
(3.7).
Konstruējot pieļaujamo apgabalu
ir mērķtiecīgi nevienādības (3.9) pārrakstīt šādi:
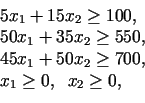 |
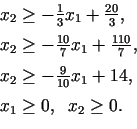 |
Pieļaujamais apgabals ir attēlots 3.3. zīmējumā.
Tātad pieļaujamā apgabala robežu veido divas koordinātu līnijas un
šādas taisnes:
taisne ![]() ar vienādojumu
ar vienādojumu
![]() ;
;
Ierobežojumiem
atbilst kopas:
![]() - pusplakne virs taisnes
- pusplakne virs taisnes ![]() ;
;
![]() - pusplakne virs taisnes
- pusplakne virs taisnes ![]() ;
;
![]() - pusplakne virs taisnes
- pusplakne virs taisnes ![]() ;
;
![]() - pusplakne, kurā
- pusplakne, kurā
![]() ;
;
![]() - pusplakne, kurā
- pusplakne, kurā
![]() .
.
Pieļaujamais apgabals - kopu
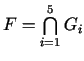 - bezgalīgs
daudzstūris.
- bezgalīgs
daudzstūris.
Mērķa funkcijas līmeņlīniju vienādojums
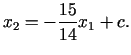 |
Kad ![]() , līmeņlīnija iet caur punktu
, līmeņlīnija iet caur punktu ![]() , kad
, kad ![]() ,
līmeņlīnija ieņem stāvokli
,
līmeņlīnija ieņem stāvokli ![]() . Secinājums: palielinot
parametru
. Secinājums: palielinot
parametru ![]() , līmeņlīnijas tiek paralēli pārnestas uz augšu. Ir
skaidrs, ka eksistē parametra
, līmeņlīnijas tiek paralēli pārnestas uz augšu. Ir
skaidrs, ka eksistē parametra ![]() vērtība, kuru apzīmēsim ar
vērtība, kuru apzīmēsim ar
![]() , kurai līmeņlīnija
, kurai līmeņlīnija
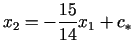 |
 |
 |
||
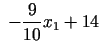 |
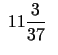 (miljonu tonnu) (miljonu tonnu) |