Atrisināsim grafiski šādu problēmu par maksimuma atrašanu.
Problēma par optimālu ražošanas plānu. Uzņēmums ražo divu veidu izstrādājumus A un B. Lai saražotu vienu izstrādājuma A vienību ir nepieciešams
Cik daudz jāsaražo A un B izstrādājumu vienību, lai peļņa būtu maksimālā?
Risinājums. Formalizēsim problēmu.
Apzīmēsim:
![]() - produkcijas A vienību daudzums (gabalos);
- produkcijas A vienību daudzums (gabalos);
![]() - produkcijas B daudzums
(gabalos).
- produkcijas B daudzums
(gabalos).
Formulēsim nosacījumus, ka materiālu noliktavā ir pietiekamā daudzumā:
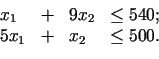 |
Mērķa funkcija - saražotās produkcijas cena:
Doto problēmu matemātiski var formulēt šādi:
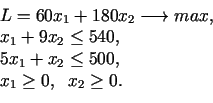 |
Lai konstruētu pieļaujamo apgabalu, pārrakstīsim ierobežojumus formā:
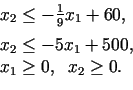 |
Pieļaujamais apgabals (skat. 3.4. zīm.) ir četrstūris
![]() , kuru veido koordinātu asis un taisnes:
, kuru veido koordinātu asis un taisnes:
taisne ![]() ar vienādojumu
ar vienādojumu
![]() ;
;
Mērķa funkcijas līmeņlīniju vienādojums:
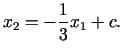 |
3.4. zīmējumā līmeņlīnija
![]() ir attēlota ar raustītu līniju. Parametram
ir attēlota ar raustītu līniju. Parametram ![]() pieaugot,
līmeņlīnijas virzās paralēli uz augšu. Skaidrs, ka punkts
pieaugot,
līmeņlīnijas virzās paralēli uz augšu. Skaidrs, ka punkts ![]() ir
pēdējais punkts, kurš ir kopīgs līmeņlīnijai un pieļaujamajam
apgabalam. Par to var arī pārliecināties, salīdzinot koeficientus
pie
ir
pēdējais punkts, kurš ir kopīgs līmeņlīnijai un pieļaujamajam
apgabalam. Par to var arī pārliecināties, salīdzinot koeficientus
pie ![]() taišņu
taišņu ![]() ,
, ![]() un
un ![]() vienādojumos:
vienādojumos:
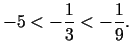 |
Lai atrastu punkta ![]() koordinātas, risinām vienādojumu sistēmu
koordinātas, risinām vienādojumu sistēmu
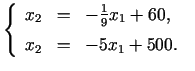 |
Atrisinājums: ![]() ,
, ![]() .
.
Iegūtā peļņa (mērķa funkcijas vērtība):
Salīdzinājumam,