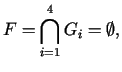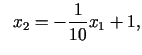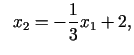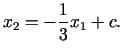Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.2.5. Uzdevumi
Augstāk: 3.2. Lineārās programēšanas uzdevumu risināšanas grafiskā
Iepriekšējais: 3.2.3. Maksimuma gadījums
Problēmai nav atrisinājuma.
Problēma.
Dotajai problēmai nav atrisinājuma, jo tās pieļaujamais apgabals
kur
Bezgalīgs pieļaujamais apgabals.
Problēma.
Dotajai problēmai nav atrisinājuma, jo mērķa funkcija nav
ierobežota pieļaujamajā apgabalā, kurš ir attēlots
3.5. zīmējumā. Atzīmēsim, ka minimizācijas
problēmai
ar tiem pašiem ierobežojumiem ir atrisinājums.
Problēmai ir bezgalīgi daudz atrisinājumu
Problēma.
Dotās problēmas pieļaujamo apgabalu (skat. 3.6. zīm.)
nosaka koordinātu asis un taisnes:
Mērķa funkcijas
līmeņlīniju vienādojums
vai
Tātad mērķa funkcijas līmeņlīnijas ir paralēlas taisnei 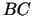 , un
līdz ar to arī pati taisne
, un
līdz ar to arī pati taisne 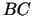 ir mērķa funkcijas līmeņlīnija.
Jebkurš nogriežņa
ir mērķa funkcijas līmeņlīnija.
Jebkurš nogriežņa 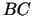 punkts (tai skaitā arī virsotnes
punkts (tai skaitā arī virsotnes 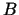 un
un
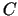 ) ir dotās problēmas atrisinājums. Tā kā nogrieznis
) ir dotās problēmas atrisinājums. Tā kā nogrieznis 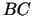 satur
bezgalīgi daudz punktu (jo
satur
bezgalīgi daudz punktu (jo 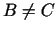 ), tad dotajai problēmai ir
bezgalīgi daudz atrisinājumu.
), tad dotajai problēmai ir
bezgalīgi daudz atrisinājumu.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.2.5. Uzdevumi
Augstāk: 3.2. Lineārās programēšanas uzdevumu risināšanas grafiskā
Iepriekšējais: 3.2.3. Maksimuma gadījums
2002-05-04