


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.3. Simpleksa metode
Augstāk: 3.2. Lineārās programēšanas uzdevumu risināšanas grafiskā
Iepriekšējais: 3.2.4. Speciālgadījumi
- 10.
Atrisināt uzdevumu
- 11.
Atrisināt uzdevumu
ar iepriekšējā uzdevuma ierobežojumiem.
- 12.
Atrisināt uzdevumu
- 13.
Atrisināt uzdevumu
ar iepriekšējā uzdevuma ierobežojumiem.
- 14.
Pieņemsim, ka uzdevumā par naftas pirkšanu nosacījumos
naftas B cena par 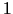 tonnu ir $
tonnu ir $ 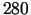 . Kādās robežās var
mainīties cena par naftas A vienu tonnu, lai atrisinājums būtu
iepriekšējais?
. Kādās robežās var
mainīties cena par naftas A vienu tonnu, lai atrisinājums būtu
iepriekšējais?
- 15.
Pieņemsim, ka problēmā par naftas pirkšanu
mainījušās cenas: naftas A cena par vienu tonnu ir $ 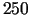 ,
naftas B cena par vienu tonnu ir $
,
naftas B cena par vienu tonnu ir $ 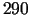 . Atrisināt uzdevumu
pie šiem nosacījumiem.
. Atrisināt uzdevumu
pie šiem nosacījumiem.
- 16.
Atrisināt uzdevumu
- 17.
Atrisināt uzdevumu
- 18.
Firma ražo divu veidu izstrādājumus A un B. Ražošanai
nepieciešamie materiāli, 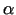 un
un 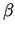 , tiek piegādāti
ierobežotā daudzumā. Cik vajag saražot izstrādājumu A un cik
izstrādājumu B, lai ienākums būtu maksimālais? Apzīmējumi:
, tiek piegādāti
ierobežotā daudzumā. Cik vajag saražot izstrādājumu A un cik
izstrādājumu B, lai ienākums būtu maksimālais? Apzīmējumi:
 - produkcijas A daudzums,
- produkcijas A daudzums,
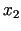 - produkcijas B daudzums,
- produkcijas B daudzums,
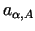 - materiāla
- materiāla 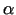 daļa vienā
izstrādājuma A
vienībā,
daļa vienā
izstrādājuma A
vienībā,
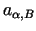 - materiāla
- materiāla 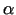 daļa vienā
izstrādājuma B
vienībā,
daļa vienā
izstrādājuma B
vienībā,
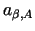 - materiāla
- materiāla 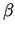 daļa vienā
izstrādājuma A
vienībā,
daļa vienā
izstrādājuma A
vienībā,
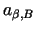 - materiāla
- materiāla 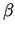 daļa vienā
izstrādājuma B
vienībā,
daļa vienā
izstrādājuma B
vienībā,
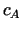 - izstrādājuma A vienas vienības cena,
- izstrādājuma A vienas vienības cena,
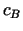 - izstrādājuma B vienas vienības cena,
- izstrādājuma B vienas vienības cena,
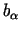 - piegādātais materiāla
- piegādātais materiāla 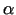 daudzums.
daudzums.
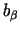 - piegādātais materiāla
- piegādātais materiāla 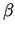 daudzums.
daudzums.
Sastādiet ražošanas procesa matemātisko modeli (formulējiet
lineārās programēšanas uzdevumu).
- 19.
Lietojiet grafisko metodi, lai atrisinātu iepriekšējo
uzdevumu šādām parametru vērtībam:



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.3. Simpleksa metode
Augstāk: 3.2. Lineārās programēšanas uzdevumu risināšanas grafiskā
Iepriekšējais: 3.2.4. Speciālgadījumi
2002-05-04