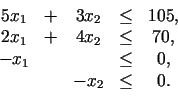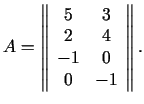Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.2. Lineārās programēšanas uzdevumu risināšanas grafiskā
Augstāk: 3. LINEĀRĀS PROGRAMMĒŠANAS UZDEVUMI
Iepriekšējais: 3. LINEĀRĀS PROGRAMMĒŠANAS UZDEVUMI
1. problēma. Aplūkosim 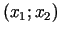 -plaknes
apgabalu, kuru nosaka nevienādības:
-plaknes
apgabalu, kuru nosaka nevienādības:
Šis apgabals ir attēlots 3.1. zīmējumā. Plaknes
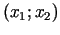 punkti, kuri apmierina nevienādību
punkti, kuri apmierina nevienādību
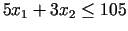 , atrodas zem taisnes
, atrodas zem taisnes 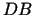 , kuras
vienādojums ir
, kuras
vienādojums ir
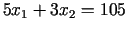 ; punkti, kuri apmierina
nevienādību
; punkti, kuri apmierina
nevienādību
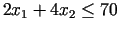 , atrodas zem taisnes
, atrodas zem taisnes 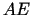 ,
kuras vienādojums ir
,
kuras vienādojums ir
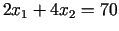 . Ņemot vērā nosacījumus
. Ņemot vērā nosacījumus
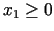 un
un
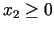 , secinām, ka apgabals, kuru nosaka
nevienādības (3.1), (3.2) un (3.3), ir
daudzstūris
, secinām, ka apgabals, kuru nosaka
nevienādības (3.1), (3.2) un (3.3), ir
daudzstūris 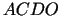 .
.
Aplūkosim taišņu saimi
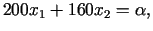 |
(3.4) |
parametram 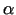 piešķirot dažādas vērtības. Ja
piešķirot dažādas vērtības. Ja 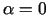 , tad
(3.4) nosaka taisni ar vienādojumu
, tad
(3.4) nosaka taisni ar vienādojumu
jeb
Šī taisne iet caur punktu 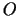 un 3.1. zīmējumā ir apzīmēta
ar
un 3.1. zīmējumā ir apzīmēta
ar 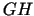 .
.
Jautājums. Kādām parametra
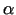 vērtībām taisne (3.4) satur kopējus punktus ar
apgabalu
vērtībām taisne (3.4) satur kopējus punktus ar
apgabalu 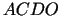 ?
?
Atrisinājums. Ja
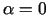 , tad taisne (3.4) ir attēlota
3.1. zīmējumā. Palielinot parametru
, tad taisne (3.4) ir attēlota
3.1. zīmējumā. Palielinot parametru 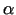 , šī taisne
virzās paralēli sev bultiņas virzienā, šķērsojot apgabalu
, šī taisne
virzās paralēli sev bultiņas virzienā, šķērsojot apgabalu 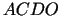 .
Acīmredzami eksistē parametra
.
Acīmredzami eksistē parametra 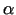 vērtība
vērtība 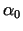 , kurai
taisne (3.4) iet caur punktu
, kurai
taisne (3.4) iet caur punktu 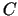 (punkts
(punkts 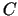 ir
daudzstūra
ir
daudzstūra 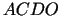 virsotne). Pie turpmākas parametra
virsotne). Pie turpmākas parametra 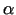 palielināšanas taisne pārvietojas uz augšu - bultiņas virzienā -
un tai vairs nav kopēju punktu ar apgabalu
palielināšanas taisne pārvietojas uz augšu - bultiņas virzienā -
un tai vairs nav kopēju punktu ar apgabalu
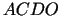 .
.
Atbilde. Maksimālā parametra
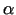 vertība, kurai taisnei
vertība, kurai taisnei
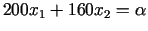 ir
kopējie punkti ar apgabalu
ir
kopējie punkti ar apgabalu 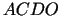 , ir vērtība
, ir vērtība 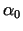 , kurai
taisne (3.4) iet caur punktu
, kurai
taisne (3.4) iet caur punktu 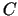 .
.
Lai atrastu 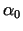 vērtību, vispirms aprēķināsim punkta
vērtību, vispirms aprēķināsim punkta 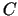 koordinātas. Tā kā
koordinātas. Tā kā 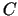 ir taišņu
ir taišņu
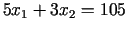 un
un
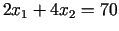 krustpunkts, tad, atrisinot lineāru vienādojumu
sistēmu
atrodam, ka punkta
krustpunkts, tad, atrisinot lineāru vienādojumu
sistēmu
atrodam, ka punkta 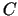 koordinātas ir
koordinātas ir 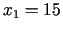 ,
, 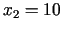 .
Ievietojot šīs koordinātas vienādojumā (3.4), iegūsim:
.
Ievietojot šīs koordinātas vienādojumā (3.4), iegūsim:
2. problēma. Uzņēmums ražo 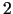 veidu izstrādājumus, kurus
apzīmēsim ar
veidu izstrādājumus, kurus
apzīmēsim ar 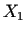 un
un 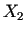 . Lai saražotu izstrādājuma
. Lai saražotu izstrādājuma 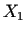 vienību, ir vajadzīgas
vienību, ir vajadzīgas 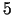 darba stundas konveijeru cehā un
darba stundas konveijeru cehā un 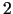 darba stundas komplektēšanas cehā. Lai saražotu izstrādātu
izstrādājuma
darba stundas komplektēšanas cehā. Lai saražotu izstrādātu
izstrādājuma 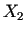 vienību, ir vajadzīgas
vienību, ir vajadzīgas 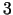 darba stundas
konveijeru cehā un
darba stundas
konveijeru cehā un 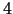 darba stundas komplektēšanas cehā.
Tehnoloģisku iemeslu dēļ mēnesī ir iespējams izmantot tikai
darba stundas komplektēšanas cehā.
Tehnoloģisku iemeslu dēļ mēnesī ir iespējams izmantot tikai 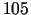 darba stundas konveijeru cehā un
darba stundas konveijeru cehā un 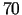 darba stundas komplektēšanas
cehā. Izstrādājuma
darba stundas komplektēšanas
cehā. Izstrādājuma 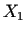 vienības cena ir Ls
vienības cena ir Ls 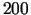 , bet
izstrādājuma
, bet
izstrādājuma 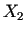 vienības cena ir
Ls
vienības cena ir
Ls 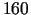 .
.
Jautājums. Cik
izstrādājumu 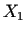 un
un 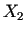 vienību ir jasaražo, lai ienākums
būtu maksimāls?
vienību ir jasaražo, lai ienākums
būtu maksimāls?
Kas saista 1. problēmu, kurai
ir ģeometriski-algebrisks raksturs, un 2. problēmu, kurai ir
ekonomisks raksturs? Abās problēmās figurē vienādi skaitļi 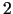 ,
,
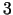 ,
, 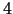 ,
, 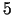 ,
, 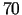 ,
, 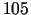 . Un vēl?
. Un vēl?
No pirmā
acu uzmetiena liekas, ka ir jāražo tikai izstrādājumi 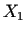 , jo
tie maksā dārgāk. Dalām skaitli
, jo
tie maksā dārgāk. Dalām skaitli 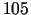 ar
ar 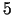 un iegūstam, ka
mēnesī konveijeru cehā var apstrādāt 1. izstrādājuma
un iegūstam, ka
mēnesī konveijeru cehā var apstrādāt 1. izstrādājuma 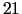 vienību.
Dalot
vienību.
Dalot 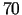 ar
ar 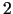 , iegūstam, ka komplektēšanas cehā var apstrādāt
, iegūstam, ka komplektēšanas cehā var apstrādāt
 izstrādājuma
izstrādājuma 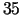 vienības. Izrādās, ka uzņēmums mēneša
laikā var saražot 1. izstrādājuma
vienības. Izrādās, ka uzņēmums mēneša
laikā var saražot 1. izstrādājuma 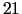 vienību, noslogojot
konveijeru cehu, bet tad komplektēšanas cehs nebūs noslogots
vienību, noslogojot
konveijeru cehu, bet tad komplektēšanas cehs nebūs noslogots 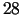 stundas (aprēķins:
stundas (aprēķins:
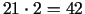 ,
, 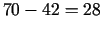 ). Ienākuma aprēķins:
). Ienākuma aprēķins:
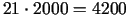 Ls. Bet vai nevarētu kopā ar 1. izstrādājumu
ražot arī zināmu daudzumu 2. izstrādājuma, lai noslogotu ražošanu?
Vai tādā gadījumā ienākums nebūtu lielāks?
Ls. Bet vai nevarētu kopā ar 1. izstrādājumu
ražot arī zināmu daudzumu 2. izstrādājuma, lai noslogotu ražošanu?
Vai tādā gadījumā ienākums nebūtu lielāks?
Tagad formulēsim 2. problēmu matemātiski. Apzīmēsim saražoto
izstrādājuma 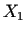 daudzumu ar
daudzumu ar  , bet saražoto
izstrādājuma
, bet saražoto
izstrādājuma 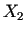 daudzumu ar
daudzumu ar 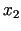 . Tad ienākumu var
aprēķināt pēc šādas formulas:
. Tad ienākumu var
aprēķināt pēc šādas formulas:
Acīmredzot,  ,
, 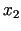 un
un 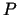 nevar pieņemt pēc patikas
lielas vērtības, jo ražošanas procesam ir ierobežojumi. Pirmais
ierobežojums:
nevar pieņemt pēc patikas
lielas vērtības, jo ražošanas procesam ir ierobežojumi. Pirmais
ierobežojums:
jo konveijeru cehā abu izstrādājumu ražošanai var izmantot ne
vairāk kā 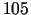 darba stundas mēnesī. Otrais ierobežojums:
darba stundas mēnesī. Otrais ierobežojums:
jo komplektēšanas cehu abu izstrādājumu ražošanai var izmantot ne
vairāk ka 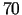 darba stundas mēnesī. Papildus ierobežojumi:
darba stundas mēnesī. Papildus ierobežojumi:
(nevar saražot negatīvu daudzumu
izstrādājumu).
Tātad ir jāatrisina šāda
matemātiska problēma:
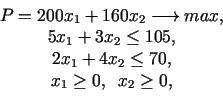 |
(3.5) |
t.i., jāatrod lineāras funkcijas maksimums ar ierobežojumiem
lineāru nevienādību formā, citiem vārdiem sakot, ir
jāatrisina tā saucamais lineārās programmēšanas
uzdevums.
Par lineārās programmēšanas
uzdevumu sauc lineāras funkcijas ekstrēma atrašanu, t.i.,
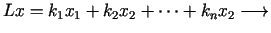 ekstrēms ekstrēms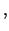 |
(3.6) |
pie lineāriem ierobežojumiem:
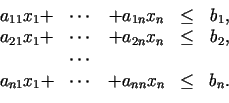 |
(3.7) |
Funkciju (3.6) sauc par mērķa
funkciju.
Piemēram, 1. problēmā funkcija
ir mērķa funkcija, kurai tiek meklēts minimums pie lineāriem
ierobežojumiem:
Šeit 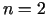 (- mainīgo skaits),
(- mainīgo skaits), 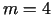 (- ierobežojumu skaits),
nevienādību (3.7) labajā pusē atrodošies skaitļi veido
vektoru
(- ierobežojumu skaits),
nevienādību (3.7) labajā pusē atrodošies skaitļi veido
vektoru
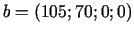 , bet nevienādību (3.7)
koeficienti
, bet nevienādību (3.7)
koeficienti 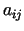 veido
veido 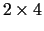 matricu
matricu



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.2. Lineārās programēšanas uzdevumu risināšanas grafiskā
Augstāk: 3. LINEĀRĀS PROGRAMMĒŠANAS UZDEVUMI
Iepriekšējais: 3. LINEĀRĀS PROGRAMMĒŠANAS UZDEVUMI
2002-05-04
![]() -plaknes
apgabalu, kuru nosaka nevienādības:
-plaknes
apgabalu, kuru nosaka nevienādības:
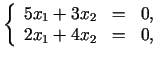
![]() veidu izstrādājumus, kurus
apzīmēsim ar
veidu izstrādājumus, kurus
apzīmēsim ar ![]() un
un ![]() . Lai saražotu izstrādājuma
. Lai saražotu izstrādājuma ![]() vienību, ir vajadzīgas
vienību, ir vajadzīgas ![]() darba stundas konveijeru cehā un
darba stundas konveijeru cehā un ![]() darba stundas komplektēšanas cehā. Lai saražotu izstrādātu
izstrādājuma
darba stundas komplektēšanas cehā. Lai saražotu izstrādātu
izstrādājuma ![]() vienību, ir vajadzīgas
vienību, ir vajadzīgas ![]() darba stundas
konveijeru cehā un
darba stundas
konveijeru cehā un ![]() darba stundas komplektēšanas cehā.
Tehnoloģisku iemeslu dēļ mēnesī ir iespējams izmantot tikai
darba stundas komplektēšanas cehā.
Tehnoloģisku iemeslu dēļ mēnesī ir iespējams izmantot tikai ![]() darba stundas konveijeru cehā un
darba stundas konveijeru cehā un ![]() darba stundas komplektēšanas
cehā. Izstrādājuma
darba stundas komplektēšanas
cehā. Izstrādājuma ![]() vienības cena ir Ls
vienības cena ir Ls ![]() , bet
izstrādājuma
, bet
izstrādājuma ![]() vienības cena ir
Ls
vienības cena ir
Ls ![]() .
.