Matemātika DU TSC
Nākamais: 3.3.3. Minimizācijas problēma Augstāk: 3.3. Simpleksa metode Iepriekšējais: 3.3.1. Izliektas kopas un lineāras programēšanas

3.3.2. Simpleksa metodes algoritms

Balstoties uz iepriekšējā paragrāfā teikto, var piedāvāt šādu lineārās programmēšanas uzdevumu risināšanas algoritmu.

1. Aprēķināt virsotņu koordinātas.
2. Aprēķināt mērķa funkcijas vērtības katrā no šiem punktiem.
3. Salīdzināt mērķa funkcijas vērtības virsotnēs un izvēlēties lielāko, ja tiek meklēts maksimums, un mazāko, ja tiek meklēts minimums.

3.1. piemērs. 

Aplūkosim $1$. problēmu (skat. šīs nodaļas ievadu). Virsotņu kopa:

$$O(0;0),\;\;A(0;17,5),\;\;C(15;10),\;\;D(21;0).$$

Mērķa funkcijas

$$P=200x_{1}+160x_{2}$$

vērtības šajos punktos:

$$P(O)=0,\;\;P(A)=2800,\;\;P(C)=4600,\;\;P(D)=4200.$$

Secinājums: $P_{max}=4600$ punktā (15;10).

Simpleksa metode pēc būtības ir pieļaujamā apgabala virsotņu pārlase, kurā tiek aplūkotas ne visas virsotnes, bet tikai tās, kurās mērķa funkcijas vērtības uzlabojas.

Apskatīsim jau iepriekš minēto $1$. problēmu (skat. šīs nodaļas ievadu):

$$P=200x_{1}+160x_{2 }\longrightarrow max,$$ (3.13)

$$5x_{1}+3x_{2}\leq 105,$$ (3.14)

$$2x_{1}+4x_{2}\leq 70,$$ (3.15)

$$x_{1}\geq 0,\;\;x_{2}\geq 0,$$ (3.16)

un atrisināsim to ar simpleksa metodi. Vispirms atzīmēsim divus būtiskus problēmas parametrus - mainīgo skaitu un ierobežojumu skaitu:
dotās problēmas mainīgo skaits - $2$,
dotās problēmas ierobežojumu skaits - $2$.

1. solis. Ievedīsim papildmainīgos, pārveidojot nevienādības vienādībās:

$$5x_{1}+3x_{2}+x_{3}=105,\;\;x_{3}\geq 0,$$ (3.17)

$$2x_{1}+4x_{2}+x_{4}=70,\;\;x_{4}\geq 0.$$ (3.18)

Atzīmēsim, ka papildmainīgie ir nenegatīvi. Modificētās problēmas dimensionalitāte $N = 4$ (četri mainīgie), bet ierobežojumu skaits $m = 2$.

2. solis. Aprēķināsim pirmās virsotnes koordinātas. Noteiksim skaitļus $x_{1}$, $x_{2}$, $x_{3}$ un $x_{4}$ tā, lai divi ($N-m=2$, problēmas dimensionalitātes un ierobežojumu skaita starpība) no tiem būtu vienādi ar nulli. Pārējo mainīgo vērtības aprēķināsim, izmantojot ierobežojumus. Mainīgo vērtības $x_{1}=0$, $x_{2}=0$, $x_{3}=105$, $x_{4}=70$ apmierina šīs prasības. Punkts ( $x_{1};x_{2})=(0;0)$ uz $(x_{1},x_{2})$-plaknes atbilst pieļaujamā apgabala virsotnei $O$.

3. solis. Izdalīsim bāzes mainīgos un izteiksim ar tiem pārējos mainīgos. Par bāzes mainīgajiem izvēlamies vienādos ar nulli mainīgos $x_{1}$ un $x_{2}$. Pārējie mainīgie veido nebāzes mainīgo kopu. Nebāzes mainīgo skaits ir vienāds ar ierobežojumu skaitu, mūsu gadījuma ar $2$ ($m = 2$), un tie ir mainīgie $x_{3}$ un $x_{4}$. Izteiksim nebāzes mainīgos ar bāzes mainīgajiem:

$$x_3= \;105-5x_1-3x_2,$$ (3.19)

$$x_4= \;70-2x_1-4x_2.$$ (3.20)

Mērķa funkcija arī tiek izteikta ar bāzes mainīgajiem:

$$P=200x_{1}+160x_{2}.$$

4. solis. Pāreja pie jaunas virsotnes. Tā kā tiek meklēts mērķa funkcijas maksimums, tad meģināsim uzlabot (palielināt) funkciju $P$, mainot vienu no mainīgajiem $x_{1}$ vai $x_{2}$. Ir svarīgi atzīmēt, ka $x_{1}$ (arī $x_{2}$) var mainīt tikai to pieaugšanas virzienā, jo $x_{1}\geq 0$ un $x_{2}\geq 0$. Mērķa funkcijas uzlabošanai ir izdevīgāk mainīt $x_{1}$, jo koeficients $200$ pie $x_{1}$ ir lielāks par koeficientu $160$ pie $x_{2}$. No nosacījuma (3.19) izriet ka $x_{1}$ var palielināt tikai līdz $21$, jo pretējā gadījumā $x_{3}$ kļūs negatīvs. No nosacījuma (3.20) izriet, ka $x_{1}$ var palielināt tikai līdz $35$, jo pretējā gadījumā $x_{4}$ kļūs negatīvs. Izvēlamies mazāko vērtību $x_{1}=21$, mainīgā $x_{2}$ vērtība paliek vienāda ar nulli, bet mainīgo $x_{3}$ un $x_{4}$ vērtības tiek aprēķinātas saskaņā ar formulām (3.19) un (3.20). Jaunā punkta koordinātas:

$$x_{1}=21,\;\;x_{2}=0,\;\;x_{3}=0,\;\;x_{4}=28.$$

Punkts $(x_{1};x_{2})=(21;0)$ uz $(x_{1};x_{2})$-plaknes atbilst pieļaujamā apgabala virsotnei $D$.

5. solis. Pēc ierobežojumu pārveidošanas mainīgais $x_{2}$ ir vienāds ar nulli, mainīgais $x_{3}$ kļuva par nulli, tātad divi ($N-m=2$) jaunie bāzes mainīgie ir $x_{2}$ un $x_{3}$. Jaunie divi ($m = 2$) nebāzes mainīgie ir $x_{1}$ un $x_{4}$. Izteiksim nebāzes mainīgos ar bāzes mainīgajiem:

$$x_{1}= \;21-\frac{3}{5}x_{2}-\frac{1}{5}x_{3},$$

$$x_{4} = \;70-2x_{1}-4x_{2},$$

jeb

$$x_{1}= \;21-\frac{3}{5}x_{2}-\frac{1}{5}x_{3},$$

$$x_{4} = \;70-2\left(21-\frac{3}{5}x_{2}-\frac{1}{5}x_{3}\right)-4x_{2},$$

jeb

$$x_{1}= \;21-\frac{3}{5}x_{2}-\frac{1}{5}x_{3},$$ (3.21)

$$x_{4} = \;28-\frac{14}{5}x_{2}+\frac{2}{5}x_{3}.$$ (3.22)

Mērķa funkcija arī tiek izteikta ar mainīgajiem $x_{2}$ un $x_{3}$:

$$P= \;200x_{1}+160x_{2}$$

$$= \;200\left(21-\frac{3}{5}x_{2}-\frac{1}{5}x_{3}\right)+160x_{2}$$

$$= \;4200+40x_{2}-40x_{3}\longrightarrow max.$$

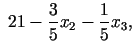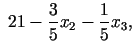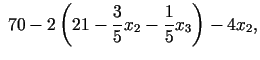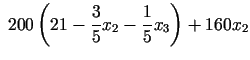6. solis. Pāreja pie jauna punkta. Tā kā koeficients pie $x_{3}$ ir negatīvs un $x_{3}\geq 0$, tad uzlabot (palielināt) mērķa funkciju var tikai palielinot $x_{2}$. No (3.21) izriet, ka $x_{2}$ var tikt palielināts tikai līdz $35$, jo pretējā gadījumā $x_{1}$ kļūtu negatīvs. No (3.20) izriet, ka $x_{2}$ var tikt palielināts tikai līdz $10$, jo pretējā gadījumā $x_{4}$ kļūtu negatīvs. Izvēlamies mazāko vērtību $x_{2}=10$, mainīgā $x_{3}$ vērtība paliek vienāda ar nulli, bet mainīgo $x_{1}$ un $x_{4}$ vērtības tiek aprēķinātas saskaņā ar formulām (3.21) un (3.22). Jaunā punkta koordinātas:

$$x_{1}=15,\;\;x_{2}=10,\;\;x_{3}=0,\;\;x_{4}=0.$$

Punkts $(x_{1};x_{2})=(15;10)$ uz $(x_{1};x_{2})$-plaknes atbilst pieļaujamā apgabala virsotnei $C$.

7. solis. Divi jaunie bāzes mainīgie: $x_{3}$ un $x_{4}$. Divi jaunie nebāzes mainīgie: $x_{1}$ un $x_{2}$. Izmantojot (3.21) un (3.22), izteiksim nebāzes mainīgos ar bāzes mainīgajiem:

$$x_{2}= \;10+\frac{1}{7}x_{3}-\frac{5}{14}x_{4},$$

$$x_1 = \;21-\frac{3}{5}\left(10+\frac{1}{7}x_{3}-\frac{5}{14}x_{4}\right)-\frac{1}{5}x_{3}$$

$$= \;15-\frac{2}{7}x_{3}+\frac{3}{14}x_{4}.$$

Mērķa funkcija arī tiek izteikta ar bāzes mainīgajiem $x_{3}$ un $x_{4}$:

$$P= \;4200x_{1}+40x_{2}-40x_{3}$$

$$= \;4200+40\left(10+\frac{1}{7}x_{3}-\frac{5}{14}x_{4}\right)-40x_{3}$$

$$= \;4200-\frac{240}{7}x_{3}-\frac{100}{7}x_{4}\longrightarrow max.$$

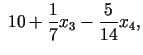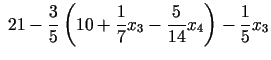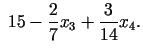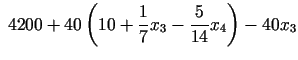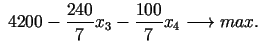8. solis. Tā kā koeficienti pie $x_{3}$ un $x_{4}$ ir negatīvi, tad uzlabot (palielināt) mērķa funkciju vairs nav iespējams, izmainot $x_{3}$ vai $x_{4}$ vērtības. Secinājums: $P_{max}=4600$ punktā $(x_{1};x_{2})=(15;10)$.

Matemātika DU TSC
Nākamais: 3.3.3. Minimizācijas problēma Augstāk: 3.3. Simpleksa metode Iepriekšējais: 3.3.1. Izliektas kopas un lineāras programēšanas