


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.3.4. Uzdevumi
Augstāk: 3.3. Simpleksa metode
Iepriekšējais: 3.3.2. Simpleksa metodes algoritms
Ilustrēsim simpleksa metodes lietošanu vēl vienas problēmas
atrisināšanai. Problēma:
1. solis. Ieved papildmainīgos 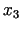 ,
, 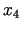 ,
,
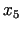 , pārveidojot nevienādības vienādībās:
, pārveidojot nevienādības vienādībās:
Modificētās problēmas dimensionalitāte 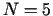 (pieci mainīgie),
bet ierobežojumu skaits
(pieci mainīgie),
bet ierobežojumu skaits 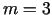 .
.
2. solis. Aprēķināsim pirmās virsotnes koordinātas.
Noteiksim skaitļus  ,
, 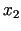 ,
, 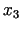 ,
, 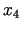 un
un 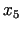 tā, lai divi (
tā, lai divi (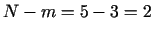 , problēmas dimensionalitātes un
ierobežojumu skaita starpība) no tiem būtu vienādi ar nulli.
Pārējo mainīgo vērtības tiks aprēķinātas, izmantojot
ierobežojumus. Kombinācija
, problēmas dimensionalitātes un
ierobežojumu skaita starpība) no tiem būtu vienādi ar nulli.
Pārējo mainīgo vērtības tiks aprēķinātas, izmantojot
ierobežojumus. Kombinācija
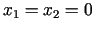 neder, jo tad
neder, jo tad
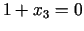 , un
, un 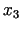 ir negatīvs. Mēģinām citu kombināciju
ir negatīvs. Mēģinām citu kombināciju
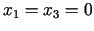 . Nosakām
. Nosakām 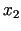 ,
, 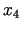 un
un 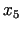 no
ierobežojumiem un iegūstam vērtības:
Visas vērtības ir nenegatīvas, tātad iegūstam pieļaujamu punktu.
Punkts
no
ierobežojumiem un iegūstam vērtības:
Visas vērtības ir nenegatīvas, tātad iegūstam pieļaujamu punktu.
Punkts
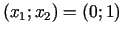 uz
uz
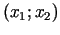 -plaknes atbilst
pieļaujamā apgabala virsotnei
-plaknes atbilst
pieļaujamā apgabala virsotnei 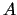 (skat. 3.7. zīm.). Tālāk,
jāpārvietojas pa pieļaujamā apgabala robežu no virsotnes uz
virsotni, uzlabojot mērķa funkcijas vērtības. Nav nozīmes, kura
virsotne bija pirmā, ir svarīgi tikai, lai tā būtu
pieļaujama (virsotne skaitās pieļaujama, ja skaitļi
(skat. 3.7. zīm.). Tālāk,
jāpārvietojas pa pieļaujamā apgabala robežu no virsotnes uz
virsotni, uzlabojot mērķa funkcijas vērtības. Nav nozīmes, kura
virsotne bija pirmā, ir svarīgi tikai, lai tā būtu
pieļaujama (virsotne skaitās pieļaujama, ja skaitļi  un
un 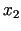 , kā arī no ierobežojumiem aprēķinātie skaitļi
, kā arī no ierobežojumiem aprēķinātie skaitļi
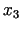 ,
, 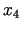 un
un 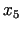 , būtu
nenegatīvi).
, būtu
nenegatīvi).
3. solis. Ierobežojumu
pārveidošana. Izdalīsim bāzes mainīgos un izteiksim ar tiem
pārējos mainīgos. Par bāzes mainīgajiem izvēlamies vienādos ar
nulli mainīgos  un
un 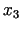 . Pārējie mainīgie veido nebāzes
mainīgo kopu. Nebāzes mainīgo skaits ir vienāds ar ierobežojumu
skaitu, mūsu gadījuma ar
. Pārējie mainīgie veido nebāzes
mainīgo kopu. Nebāzes mainīgo skaits ir vienāds ar ierobežojumu
skaitu, mūsu gadījuma ar 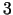 (
(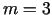 ), un tie ir
), un tie ir 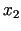 ,
, 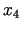 un
un 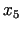 . Izteiksim nebāzes mainīgos ar bāzes mainīgajiem:
. Izteiksim nebāzes mainīgos ar bāzes mainīgajiem:
jeb
jeb
Mērķa funkcija arī tiek izteikta ar bāzes mainīgajiem:
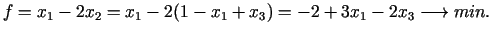 |
(3.26) |
4. solis. Jaunas virsotnes meklēšana. Tā kā tiek meklēts
mērķa funkcijas minimums, mēģināsim uzlabot (samazināt) funkciju
 , mainot vienu no bāzes mainīgajiem
, mainot vienu no bāzes mainīgajiem  vai
vai 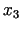 .
Aplūkosim abus variantus. Tā kā
.
Aplūkosim abus variantus. Tā kā
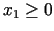 un tekošā
un tekošā  vērtība ir nulle, tad mainīt
vērtība ir nulle, tad mainīt  nevar, jo koeficients pie
nevar, jo koeficients pie
 formulā (3.26) ir pozitīvs un tāpēc funkcijas
formulā (3.26) ir pozitīvs un tāpēc funkcijas  vērtības var tikai pieaugt. Samazināt mērķa funkciju var mainot
vērtības var tikai pieaugt. Samazināt mērķa funkciju var mainot
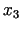 . No nosacījuma (3.24) izriet, ka
. No nosacījuma (3.24) izriet, ka 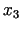 var
palielināt tikai līdz
var
palielināt tikai līdz 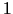 , jo pretējā gadījumā
, jo pretējā gadījumā 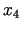 kļūs
negatīvs. No nosacījuma (3.25) izriet, ka
kļūs
negatīvs. No nosacījuma (3.25) izriet, ka 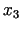 var
palielināt tikai līdz
var
palielināt tikai līdz 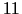 , jo pretējā gadījumā
, jo pretējā gadījumā 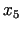 kļūs
negatīvs. Izvēlamies mazāko vērtību
kļūs
negatīvs. Izvēlamies mazāko vērtību 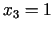 un aprēķinām jaunās
un aprēķinām jaunās
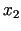 ,
, 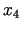 un
un 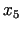 vērtības. Jaunā punkta koordinātas:
vērtības. Jaunā punkta koordinātas:
Punkts
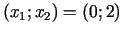 uz
uz
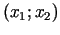 -plaknes atbilst
pieļaujamā apgabala virsotnei
-plaknes atbilst
pieļaujamā apgabala virsotnei 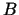 .
.
5. solis. Cikla atkārtošana. Pēc ierobežojumu
pārveidošanas mainīgais  ir vienāds ar nulli, mainīgais
ir vienāds ar nulli, mainīgais
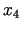 kļuva par nulli, tātad divi (
kļuva par nulli, tātad divi (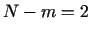 ) jaunie bāzes
mainīgie ir
) jaunie bāzes
mainīgie ir  un
un 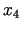 . Jaunie trīs (
. Jaunie trīs (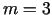 ) nebāzes
mainīgie ir
) nebāzes
mainīgie ir 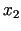 ,
, 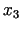 un
un 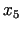 . Izteiksim nebāzes
mainīgos ar mainīgajiem. Izmantojot (3.24), atrodam
. Izteiksim nebāzes
mainīgos ar mainīgajiem. Izmantojot (3.24), atrodam
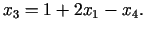 |
(3.27) |
Izmantojot (3.23) un (3.27), iegūsim:
jeb
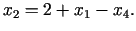 |
(3.28) |
Izmantojot (3.25) un (3.27), atrodam
jeb
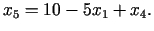 |
(3.29) |
Mērķa funkcija arī tiek izteikta ar mainīgajiem  un
un
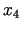 :
:
6. solis. Pāreja pie jauna punkta. Tā kā koeficients pie
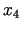 ir pozitīvs un
ir pozitīvs un
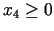 , tad uzlabot (samazināt)
mērķa funkciju var tikai palielinot
, tad uzlabot (samazināt)
mērķa funkciju var tikai palielinot  . No (3.29)
izriet, ka
. No (3.29)
izriet, ka  var būt palielināts tikai līdz
var būt palielināts tikai līdz 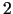 , jo pretējā
gadījumā
, jo pretējā
gadījumā 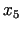 kļūs negatīvs. Vienādībās (3.27) un
(3.28) mainīgais
kļūs negatīvs. Vienādībās (3.27) un
(3.28) mainīgais  ietilpst ar pozitīviem
koeficientiem un tāpēc var būt palielināts līdz bezgalībai.
Izvēlamies mazāko vērtību
ietilpst ar pozitīviem
koeficientiem un tāpēc var būt palielināts līdz bezgalībai.
Izvēlamies mazāko vērtību 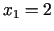 ,
, 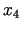 paliek nulle, bet
paliek nulle, bet
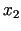 ,
, 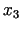 un
un 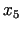 tiek aprēķināti pēc formulām
(3.27), (3.28) un (3.29). Jaunā punkta
koordinātas:
tiek aprēķināti pēc formulām
(3.27), (3.28) un (3.29). Jaunā punkta
koordinātas:
Punkts
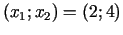 uz
uz
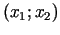 -plaknes atbilst
pieļaujamā apgabala virsotnei
-plaknes atbilst
pieļaujamā apgabala virsotnei 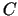 .
.
7. solis. Divi jaunie bāzes mainīgie: 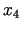 un
un 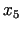 .
Trīs jaunie nebāzes mainīgie:
.
Trīs jaunie nebāzes mainīgie:  ,
, 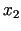 un
un 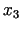 .
Izteiksim nebāzes mainīgos ar bāzes mainīgajiem. Izmantojot
formulas (3.27), (3.28) un (3.29),
iegūstam:
.
Izteiksim nebāzes mainīgos ar bāzes mainīgajiem. Izmantojot
formulas (3.27), (3.28) un (3.29),
iegūstam:
Mērķa funkcija arī tiek izteikta ar nebāzes mainīgajiem 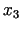 un
un
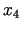 :
:
8. solis. Tā kā koeficienti pie 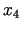 un
un 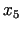 ir
pozitīvi, tad uzlabot (samazināt) mērķa funkciju vairs nav
iespējams, mainot
ir
pozitīvi, tad uzlabot (samazināt) mērķa funkciju vairs nav
iespējams, mainot 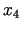 vai
vai 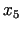 . Secinājums:
. Secinājums:
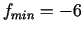 punktā
punktā
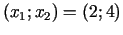 .
.
-
3.1. piezīme.
- Simpleksa metodes aprakstu, analīzi, vēsturi un
diskusijas par to var atrast grāmatā [1].



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.3.4. Uzdevumi
Augstāk: 3.3. Simpleksa metode
Iepriekšējais: 3.3.2. Simpleksa metodes algoritms
2002-05-04
![]() ,
, ![]() ,
,
![]() , pārveidojot nevienādības vienādībās:
, pārveidojot nevienādības vienādībās:
![]() , mainot vienu no bāzes mainīgajiem
, mainot vienu no bāzes mainīgajiem ![]() vai
vai ![]() .
Aplūkosim abus variantus. Tā kā
.
Aplūkosim abus variantus. Tā kā
![]() un tekošā
un tekošā ![]() vērtība ir nulle, tad mainīt
vērtība ir nulle, tad mainīt ![]() nevar, jo koeficients pie
nevar, jo koeficients pie
![]() formulā (3.26) ir pozitīvs un tāpēc funkcijas
formulā (3.26) ir pozitīvs un tāpēc funkcijas ![]() vērtības var tikai pieaugt. Samazināt mērķa funkciju var mainot
vērtības var tikai pieaugt. Samazināt mērķa funkciju var mainot
![]() . No nosacījuma (3.24) izriet, ka
. No nosacījuma (3.24) izriet, ka ![]() var
palielināt tikai līdz
var
palielināt tikai līdz ![]() , jo pretējā gadījumā
, jo pretējā gadījumā ![]() kļūs
negatīvs. No nosacījuma (3.25) izriet, ka
kļūs
negatīvs. No nosacījuma (3.25) izriet, ka ![]() var
palielināt tikai līdz
var
palielināt tikai līdz ![]() , jo pretējā gadījumā
, jo pretējā gadījumā ![]() kļūs
negatīvs. Izvēlamies mazāko vērtību
kļūs
negatīvs. Izvēlamies mazāko vērtību ![]() un aprēķinām jaunās
un aprēķinām jaunās
![]() ,
, ![]() un
un ![]() vērtības. Jaunā punkta koordinātas:
vērtības. Jaunā punkta koordinātas:
![]() ir pozitīvs un
ir pozitīvs un
![]() , tad uzlabot (samazināt)
mērķa funkciju var tikai palielinot
, tad uzlabot (samazināt)
mērķa funkciju var tikai palielinot ![]() . No (3.29)
izriet, ka
. No (3.29)
izriet, ka ![]() var būt palielināts tikai līdz
var būt palielināts tikai līdz ![]() , jo pretējā
gadījumā
, jo pretējā
gadījumā ![]() kļūs negatīvs. Vienādībās (3.27) un
(3.28) mainīgais
kļūs negatīvs. Vienādībās (3.27) un
(3.28) mainīgais ![]() ietilpst ar pozitīviem
koeficientiem un tāpēc var būt palielināts līdz bezgalībai.
Izvēlamies mazāko vērtību
ietilpst ar pozitīviem
koeficientiem un tāpēc var būt palielināts līdz bezgalībai.
Izvēlamies mazāko vērtību ![]() ,
, ![]() paliek nulle, bet
paliek nulle, bet
![]() ,
, ![]() un
un ![]() tiek aprēķināti pēc formulām
(3.27), (3.28) un (3.29). Jaunā punkta
koordinātas:
tiek aprēķināti pēc formulām
(3.27), (3.28) un (3.29). Jaunā punkta
koordinātas:
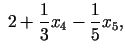
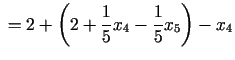

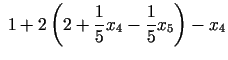
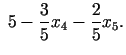
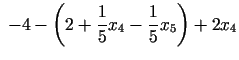
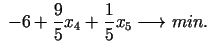
![]() un
un ![]() ir
pozitīvi, tad uzlabot (samazināt) mērķa funkciju vairs nav
iespējams, mainot
ir
pozitīvi, tad uzlabot (samazināt) mērķa funkciju vairs nav
iespējams, mainot ![]() vai
vai ![]() . Secinājums:
. Secinājums:
![]() punktā
punktā
![]() .
.