Matemātika DU TSC
Nākamais: ATBILDES Augstāk: 3.3.3. Minimizācijas problēma Iepriekšējais: 3.3.3. Minimizācijas problēma

3.3.4. Uzdevumi

20.

Atrisināt uzdevumu

$$f(x_{1};x_{2};x_{3};x_{4})=x_{1}+1,2x_{2}+2x_{3}+1,8x_{4}\longrightarrow min,$$

$$x_{1 }+ x_{2}\leq 15,\;\;x_{3}+ x_{4}\leq 60,\;\; x_{1}+ x_{3}\geq 20,\;\; x_{2 }+ x_{4}\geq 40,$$

$$x_{1 }\geq 0,\;\; x_{2}\geq 0,\;\; x_{3}\geq 0,\;\; x_{4 }\geq 0.$$

21.

Atrisināt uzdevumu

$$f(x_{1};x_{2};x_{3})=\longrightarrow max,$$

$$x_{1}+x_{2}+x_{3 } \leq 1,\;\; x_{1 }\geq 0,\;\; x_{2}\geq 0,\;\; x_{3}\geq 0.$$

šādam funkcijām f:

21a.

$f(x_{1};x_{2};x_{3}) = 2 x_{1 }+ x_{2}$;

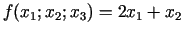21b.

$f(x_{1};x_{2};x_{3}) = 3 x_{1 } - 2x_{2}$;

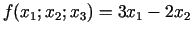21c.

$f(x_{1};x_{2};x_{3}) = 3 x_{1 } - x_{2}$;

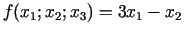21d.

$f(x_{1};x_{2};x_{3}) = 2 x_{1 }+ 3x_{2}$;

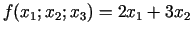21e.

$f(x_{1};x_{2};x_{3}) = x_{1 } - 4x_{3}$;

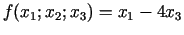21f.

$f(x_{1};x_{2};x_{3}) = x_{1}-x_{2}+x_{3}$;

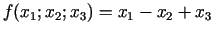21g.

$f(x_{1};x_{2};x_{3}) = 2x_{1}-x_{2}+x_{3}$;

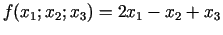21h.

$f(x_{1};x_{2};x_{3}) = x_{1 } - x_{2 }+3x_{3}$;

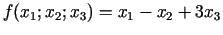21i.

$f(x_{1};x_{2};x_{3}) = 2 x_{1} - x_{3}$.

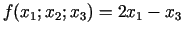22.

Atrisināt uzdevumu

$$L=5x_{1}+12x_{2}\longrightarrow min,$$

$$x_{1} + 2 x_{2 }\geq 6,$$

$$x_{1} + 3 x_{2 } \geq 8,$$

$$x_{1} + 6 x_{2 } \geq 11,$$

$$x_{1}\geq 0,\;\;x_{2}\geq 0.$$

ar simpleksa metodi.

22.

Atrisināt uzdevumu

$$L=3x_{1}+12x_{2}\longrightarrow min$$

ar iepriekšējā uzdevuma ierobežojumiem.

Matemātika DU TSC
Nākamais: ATBILDES Augstāk: 3.3.3. Minimizācijas problēma Iepriekšējais: 3.3.3. Minimizācijas problēma