


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: LITERATŪRA
Augstāk: optfs
Iepriekšējais: 3.3.4. Uzdevumi
1. 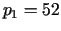 ,
, 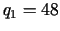 ,
, 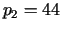 ,
, 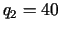 .
.
2. 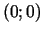 ir minimuma punkts, punktā
ir minimuma punkts, punktā
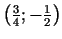 ekstrēma nav.
ekstrēma nav.
3a.
Punktā 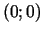 ekstrēma nav,
ekstrēma nav,
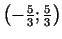 ir maksimuma punkts.
ir maksimuma punkts.
3b. Punktā 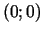 ekstrēma nav,
ekstrēma nav, 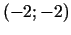 ir maksimuma
punkts.
ir maksimuma
punkts.
3c. Punktā
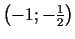 ekstrēma nav.
ekstrēma nav.
3d. 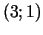 ir minimuma punkts.
ir minimuma punkts.
4.
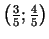 .
.
5.
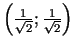 ,
,
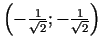 .
.
6a.
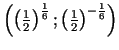 un
un
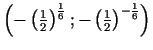 .
.
6b.
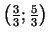 ,
,
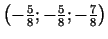 .
.
6c. 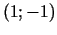 .
.
6d.
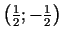 .
.
6e.
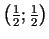 .
.
6f. 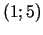 un
un
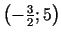 .
.
7a.
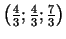 ,
,
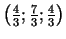 un
un
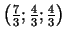 ir
maksimuma punkti;
ir
maksimuma punkti; 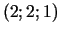 ,
, 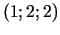 un
un 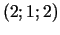 ir
minimuma punkti.
ir
minimuma punkti.
7b.
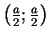 ir maksimuma punkts.
ir maksimuma punkts.
7c. 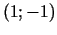 ir minimuma punkts.
ir minimuma punkts.
7d.
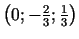 ir minimuma punkts.
ir minimuma punkts.
7e.
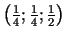 ir
minimuma punkts.
ir
minimuma punkts.
8a. 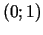 un
un 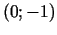 ir maksimuma
punkti;
ir maksimuma
punkti;
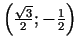 un
un
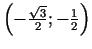 ir minimuma punkti.
ir minimuma punkti.
8b.
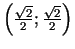 un
un
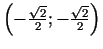 ir
maksimuma punkti;
ir
maksimuma punkti;
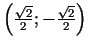 un
un
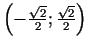 ir minimuma punkti.
ir minimuma punkti.
8c.
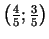 ir minimuma punkts,
ir minimuma punkts,
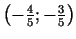 ir maksimuma punkts.
ir maksimuma punkts.
8d. 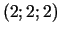 ir minimuma punkts.
ir minimuma punkts.
9. 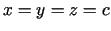 .
.
10. 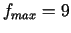 punktā
punktā 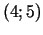 .
.
11.
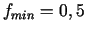 punktā
punktā 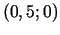 .
.
12.
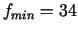 punktā
punktā
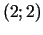 .
.
13.
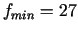 punktā
punktā 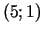 .
.
14. ![$ [252;400]$](img1115.gif) .
.
15.
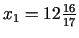 mln. t.,
mln. t.,
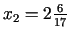 mln. t.
mln. t.
16.
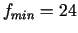 visos segmenta
visos segmenta
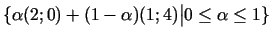 punktos.
punktos.
17. 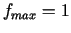 punktā
punktā 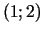 .
.
18.
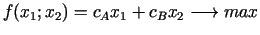 ,
,
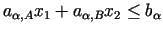 ,
,
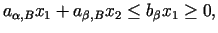
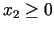 .
.
19. 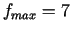 punktā
punktā 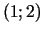 .
.
20.
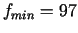 punktā
punktā
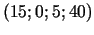 .
.
21a.
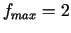 punktā
punktā 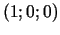 .
.
21b. 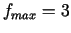 punktā
punktā
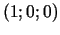 .
.
21c. 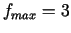 punktā
punktā 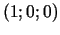 .
.
21d. 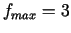 punktā
punktā 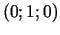 .
.
21e.
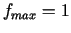 punktā
punktā 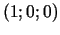 .
.
21f. 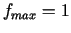 visos
segmenta
visos
segmenta
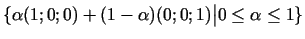 punktos.
punktos.
21g. 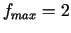 punktā
punktā
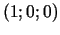 .
.
21h. 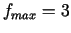 punktā
punktā 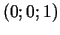 .
.
21i. 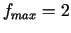 punktā
punktā 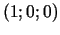 .
.
22. (2;2).
23. (5;1).



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: LITERATŪRA
Augstāk: optfs
Iepriekšējais: 3.3.4. Uzdevumi
2002-05-04
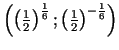 un
un
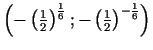 .
.
![]()
![]()
![]()
![]() Matemātika
DU TSC
Matemātika
DU TSC