


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.8. Uzdevumi
Augstāk: 3.5. Logaritmiskās funkcijas definēšana ar integrāli
Iepriekšējais: 3.6. Jautājumi
- Pierādīt 1. un 2.
īpašības sekas.
- Pamatot primitīvās funkcijas eksistenci katrai intervālā
![$ [a;b]$](img524.gif) nepārtrauktai funkcijai.
nepārtrauktai funkcijai.
- Formulēt un pierādīt teorēmas par integrāļa ar mainīgu
apakšējo robežu nepārtrauktību un diferencēšanu.
- Atvasināt šādas funkcijas:
-
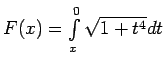 ;
;
-
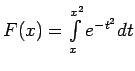 .
.
- Aprēķināt šādus noteiktos integrāļus:
-
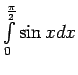 ;
;
-
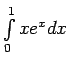 ;
;
-
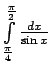 .
.
- Sniegt ģeometrisko interpretāciju integrālim no pāra vai
nepāra funkcijas intervālā
![$ [-a;a]$](img844.gif) .
.
- Formulēt un pamatot funkcijas
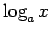 svarīgākās īpašības.
svarīgākās īpašības.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.8. Uzdevumi
Augstāk: 3.5. Logaritmiskās funkcijas definēšana ar integrāli
Iepriekšējais: 3.6. Jautājumi
2002-11-06
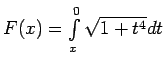 ;
;
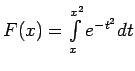 .
.
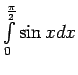 ;
;
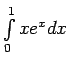 ;
;
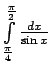 .
.
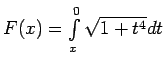 ;
;
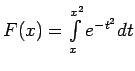 .
.
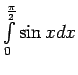 ;
;
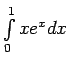 ;
;
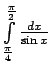 .
.