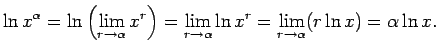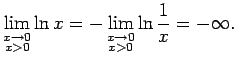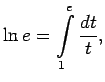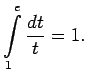Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.6. Jautājumi
Augstāk: 3. INTEGRĀLIS AR MAINĪGU AUGŠĒJO ROBEŽU
Iepriekšējais: 3.4. Integrāļi no pāra vai nepāra
Visbiežāk logaritmisko funkciju definē kā apvērsto funkciju
eksponentfunkcijai. Taču logaritmisko funkciju var
definēt arī kā integrāli ar mainīgu augšējo integrēšanas robežu,
t.i.,
Atliek parādīt, ka no šīs definīcijas un integrāļa īpašībām seko
visas logaritmiskās funkcijas īpašības.
- Definīcijas apgabals (norādīts definīcijā) ir intervāls
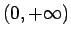 .
.
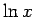 ir nepārtraukta funkcija kā integrālis ar mainīgu
augšējo robežu no nepārtrauktas (integrējamas) funkcijas
ir nepārtraukta funkcija kā integrālis ar mainīgu
augšējo robežu no nepārtrauktas (integrējamas) funkcijas
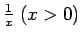 .
.
- Atrod
Visiem
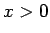
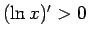 , tas nozīmē, ka
, tas nozīmē, ka 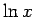 ir augoša
funkcija.
ir augoša
funkcija.
- Atrod
tātad
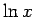 ir izliekta funkcija.
ir izliekta funkcija.
- Atrod
- Apskata
Tātad
Atrod
Tātad
Atrod
Tātad
- Parāda, ka
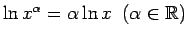 .
.
- Ja
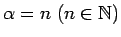 , tad
, tad
- Ja
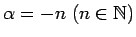 , tad
, tad
- Ja
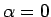 , tad
Tātad jebkuram veselam skaitlim
, tad
Tātad jebkuram veselam skaitlim
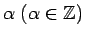 ir
spēkā vienādība
ir
spēkā vienādība
- Ja
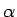 ir racionāls skaitlis (
ir racionāls skaitlis (
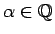 ), tad
Apskata vispirms
Tātad
Apskata
), tad
Apskata vispirms
Tātad
Apskata
- Ja
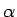 ir iracionāls skaitlis (
ir iracionāls skaitlis (
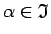 ),
tad saskaņā ar pozitīva skaitļa
),
tad saskaņā ar pozitīva skaitļa 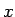 pakāpes ar iracionālu
kāpinātāju definīciju
kur
pakāpes ar iracionālu
kāpinātāju definīciju
kur
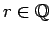 .
.
Tātad
(Tika izmantota logaritmiskās funkcijas nepārtrauktība). Tādējādi
jebkuram
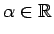 ir spēkā vienādība
ir spēkā vienādība
- Tā kā
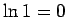 un
un 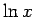 ir augoša funkcija, tad
ir augoša funkcija, tad 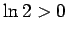 .
.
Ja 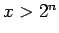 , tad
, tad
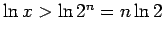 . Seko, ka
. Seko, ka
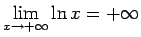 .
.
Tā kā
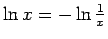 , tad
Tātad
, tad
Tātad 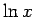 pieņem jebkuras negatīvas un jebkuras pozitīvas
vērtības. Tādējādi
pieņem jebkuras negatīvas un jebkuras pozitīvas
vērtības. Tādējādi 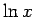 vērtību apgabals ir intervāls
vērtību apgabals ir intervāls
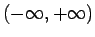 .
.
Saskaņā ar Bolcano-Košī teorēmu par nepārtrauktas funkcijas
starpvērtībām eksistē tāda vērtība, kuru apzīmē ar 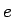 , ka
, ka 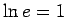 (pie tam tāda vērtība ir vienīgā, jo
(pie tam tāda vērtība ir vienīgā, jo 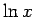 ir augoša
funkcija).
ir augoša
funkcija).
Tā kā
tad
No ģeometriskā viedokļa tas nozīmē, ka atbilstošai līklīnijas
trapecei, kuru no augšas ierobežo hiperbolas
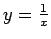 zars,
laukums ir
zars,
laukums ir 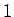 (3.1. zīm.).
(3.1. zīm.).
- Apskata
Tas nozīmē, ka ar integrāli definētā logaritmiskā funkcija ir
eksponentfunkcijai apvērstā funkcija.
- Piezīme.
- Logaritmisko funkciju ar patvaļīgu bāzi
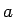 definē
šādi:
definē
šādi:
No šīs definīcijas un funkcijas 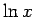 īpašībām izriet funkcijas
īpašībām izriet funkcijas
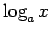 atbilstošās īpašības.
atbilstošās īpašības.
(Iegūt un pamatot šīs īpašības patstāvīgi).



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.6. Jautājumi
Augstāk: 3. INTEGRĀLIS AR MAINĪGU AUGŠĒJO ROBEŽU
Iepriekšējais: 3.4. Integrāļi no pāra vai nepāra
2002-11-06
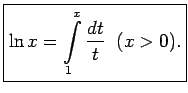
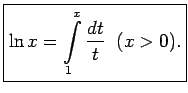
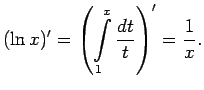
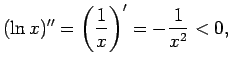
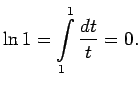
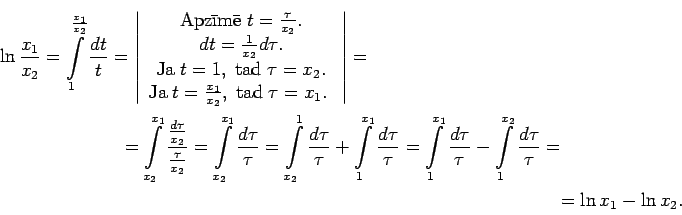
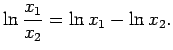
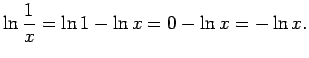
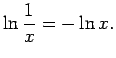
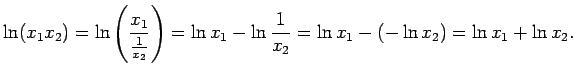
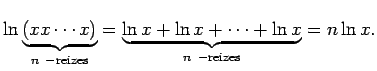
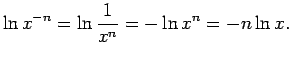
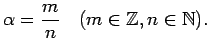
![$\displaystyle \ln\sqrt[n]{x}=\frac{1}{n}\ln x\/.$](img879.gif)
![$\displaystyle \ln x^r=\ln x^{\frac{m}{n}}=\ln\left(\sqrt[n]{x}\right)^m=
m\ln\sqrt[n]{x}=m\frac{1}{n}\ln x=\frac{m}{n}\ln x=r\ln x\/.$](img880.gif)