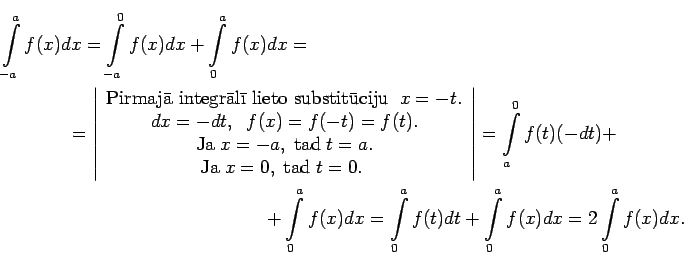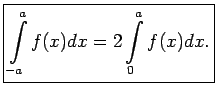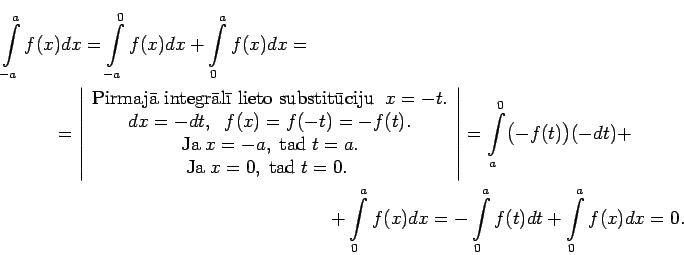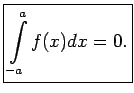Matemātika DU TSC
Nākamais: 3.5. Logaritmiskās funkcijas definēšana ar integrāli Augstāk: 3. INTEGRĀLIS AR MAINĪGU AUGŠĒJO ROBEŽU Iepriekšējais: 3.3.2. Integrēšana ar mainīgā aizvietošanu

3.4. Integrāļi no pāra vai nepāra funkcijas

Apskata intervālā $[-a;a]$ (simetriska attiecībā pret nulli kopa) integrējamu funkciju $f$.

1. Pieņem, ka $f$ ir pāra funkcija, t.i., visiem $x\in[-a;a]$ izpildās sakarība $f(-x)=f(x)$.
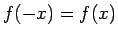   Apskata
   $$\begin{multline*} \int\limits_{-a}^af(x)dx=\int\limits_{-a}^0f(x)dx+\int\limits... ...\limits_0^af(t)dt+\int\limits_0^af(x)dx=2\int\limits_0^af(x)dx. \end{multline*}$$
   
   
   Tādējādi pāra funkcijai $f$ ir spēkā vienādība
   $$\boxed{\int\limits_{-a}^af(x)dx=2\int\limits_0^af(x)dx.}$$

2. Pieņem, ka $f$ ir nepāra funkcija, t.i., visiem $x\in[-a;a]$ izpildās sakarība $f(-x)=-f(x)$.
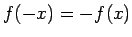   Apskata
   $$\begin{multline*} \int\limits_{-a}^af(x)dx=\int\limits_{-a}^0f(x)dx+\int\limits... ...imits_0^af(x)dx=-\int\limits_0^af(t)dt+\int\limits_0^af(x)dx=0. \end{multline*}$$
   
   
   Tādējādi nepāra funkcijai $f$ ir spēkā vienādība
   $$\boxed{\int\limits_{-a}^af(x)dx=0.}$$

Matemātika DU TSC
Nākamais: 3.5. Logaritmiskās funkcijas definēšana ar integrāli Augstāk: 3. INTEGRĀLIS AR MAINĪGU AUGŠĒJO ROBEŽU Iepriekšējais: 3.3.2. Integrēšana ar mainīgā aizvietošanu