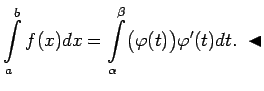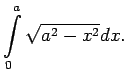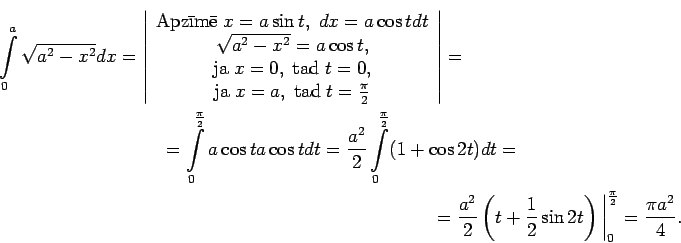Ja funkcija
![]() ir nepārtraukti diferencējama intervālā ar
galapunktiem
ir nepārtraukti diferencējama intervālā ar
galapunktiem ![]() ,
, ![]() un attēlo šo intervālu par intervālu
ar galapunktiem
un attēlo šo intervālu par intervālu
ar galapunktiem
![]() ,
,
![]() , kurā ir
definēta nepārtraukta funkcija
, kurā ir
definēta nepārtraukta funkcija ![]() , tad ir spēkā formula:
, tad ir spēkā formula:
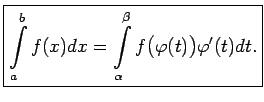
Ja funkcija
![]() ir nepārtraukti diferencējama intervālā ar
galapunktiem
ir nepārtraukti diferencējama intervālā ar
galapunktiem ![]() ,
, ![]() un attēlo šo intervālu par intervālu
ar galapunktiem
un attēlo šo intervālu par intervālu
ar galapunktiem
![]() ,
,
![]() , kurā ir
definēta nepārtraukta funkcija
, kurā ir
definēta nepārtraukta funkcija ![]() , tad ir spēkā formula:
, tad ir spēkā formula:
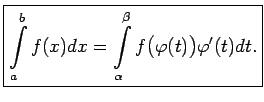
![]() Apskata divas palīgfunkcijas
Apskata divas palīgfunkcijas
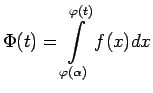 un
un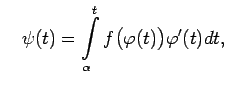
Acīmredzami
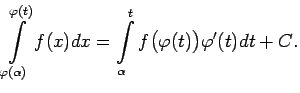
Ievieto ![]() un iegūst, ka
un iegūst, ka ![]() . Tātad
. Tātad
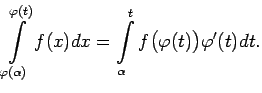
Ievieto ![]() .
.
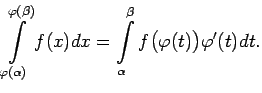
Tā kā
![]() un
un
![]() , tad
, tad