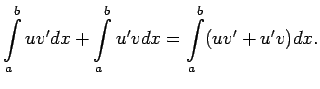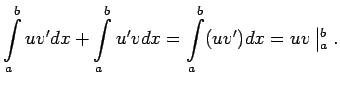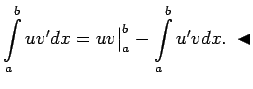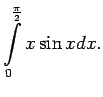Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.3.2. Integrēšana ar mainīgā aizvietošanu
Augstāk: 3.3. Integrēšanas pamatmetodes noteiktajā integrālī
Iepriekšējais: 3.3. Integrēšanas pamatmetodes noteiktajā integrālī
-
3.1. definīcija.
- Funkciju
 sauc par nepārtraukti
diferencējamu intervālā
sauc par nepārtraukti
diferencējamu intervālā
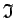 , ja tai eksistē šajā intervālā
nepārtraukts atvasinājums.
, ja tai eksistē šajā intervālā
nepārtraukts atvasinājums.
-
3.2. teorēma.
- [Parciālā integrēšana noteiktajā integrālī]
Ja 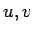 ir nepārtraukti diferencējamas funkcijas intervālā
ir nepārtraukti diferencējamas funkcijas intervālā ![$ [a;b]$](img524.gif) ,
tad
,
tad
jeb
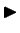 Visi integrāļi eksistē, jo zemintegrāļu
funkcijas ir nepārtrauktas.
Visi integrāļi eksistē, jo zemintegrāļu
funkcijas ir nepārtrauktas.
Apskata
Tā kā
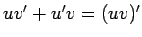 , tad
Tādējādi
, tad
Tādējādi
-
3.2. piemērs.
- Aprēķināt



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.3.2. Integrēšana ar mainīgā aizvietošanu
Augstāk: 3.3. Integrēšanas pamatmetodes noteiktajā integrālī
Iepriekšējais: 3.3. Integrēšanas pamatmetodes noteiktajā integrālī
2002-11-06
![]() ir nepārtraukti diferencējamas funkcijas intervālā
ir nepārtraukti diferencējamas funkcijas intervālā ![]() ,
tad
,
tad
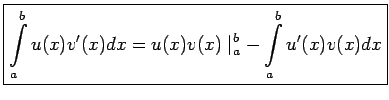
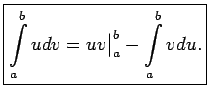
![]() Visi integrāļi eksistē, jo zemintegrāļu
funkcijas ir nepārtrauktas.
Visi integrāļi eksistē, jo zemintegrāļu
funkcijas ir nepārtrauktas.