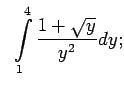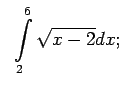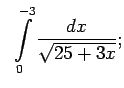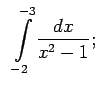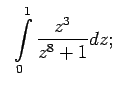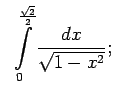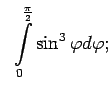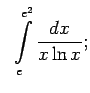Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4. KVADRĒJAMĪBAS KRITĒRIJI
Augstāk: 3.5. Logaritmiskās funkcijas definēšana ar integrāli
Iepriekšējais: 3.7. Vingrinājumi
- Izmantojot Ņūtona-Leibnica formulu, aprēķināt šādus noteiktos
integrāļus:
| (a) |
![$\displaystyle \;\;\int\limits_0^8\left(\sqrt{2x}+\sqrt[3]{x}\right)dx;$](img909.gif) |
(b) |
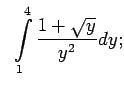 |
|
| (c) |
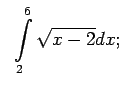 |
(d) |
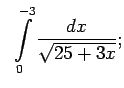 |
|
| (e) |
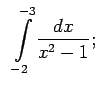 |
(f) |
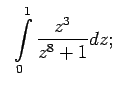 |
|
| (g) |
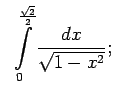 |
(h) |
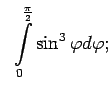 |
|
| (i) |
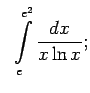 |
(j) |
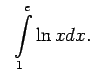 |
|
- Izmantojot noteiktos integrāļus, aprēķināt šādas robežas:
-
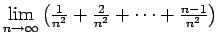 ,
,
-
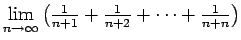 .
.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4. KVADRĒJAMĪBAS KRITĒRIJI
Augstāk: 3.5. Logaritmiskās funkcijas definēšana ar integrāli
Iepriekšējais: 3.7. Vingrinājumi
2002-11-06
![$\displaystyle \;\;\int\limits_0^8\left(\sqrt{2x}+\sqrt[3]{x}\right)dx;$](img909.gif)
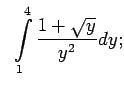
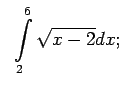
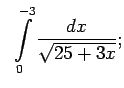
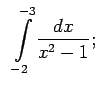
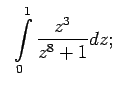
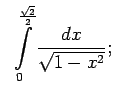
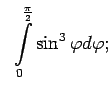
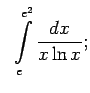
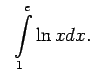
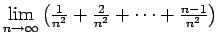 ,
,
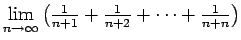 .
.
![$\displaystyle \;\;\int\limits_0^8\left(\sqrt{2x}+\sqrt[3]{x}\right)dx;$](img909.gif)