


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.2. Sakarība starp noteikto un nenoteikto
Augstāk: 3. INTEGRĀLIS AR MAINĪGU AUGŠĒJO ROBEŽU
Iepriekšējais: 3. INTEGRĀLIS AR MAINĪGU AUGŠĒJO ROBEŽU
Ja  ir intervālā
ir intervālā ![$ [a;b]$](img524.gif) integrējama funkcija, tad saskaņā ar
noteiktā integrāļa 2. īpašību tā ir
integrējama katrā no intervāliem
integrējama funkcija, tad saskaņā ar
noteiktā integrāļa 2. īpašību tā ir
integrējama katrā no intervāliem ![$ [a;x]$](img783.gif) (
(![$ x\in[a;b]$](img664.gif) ), pie tam
šāda integrāļa vērtība ir atkarīga no
), pie tam
šāda integrāļa vērtība ir atkarīga no 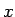 .
.
Tādējādi integrālis ar mainīgu augšējo robežu ir šīs augšējās robežas
funkcija, t.i.,
- 1. īpašība.
- [Integrāļa ar mainīgu augšējo robežu
nepārtrauktība]
Ja  ir intervālā
ir intervālā ![$ [a;b]$](img524.gif) integrējama funkcija, tad
integrējama funkcija, tad
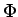 ir
nepārtraukta šajā intervālā funkcija.
ir
nepārtraukta šajā intervālā funkcija.
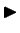 Izvēlas patvaļīgu
Izvēlas patvaļīgu ![$ x\in[a;b]$](img664.gif) un patvaļīgu
un patvaļīgu
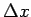 , bet tādu, lai
, bet tādu, lai
![$ x+\Delta x\in[a;b]$](img787.gif) , un apskata
, un apskata
kur
![$ M=\sup\limits_{[a;b]}\vert f(x)\vert$](img790.gif) . (Tāda galīga vērtība eksistē,
jo
. (Tāda galīga vērtība eksistē,
jo  ir ierobežota kā integrējama funkcija).
ir ierobežota kā integrējama funkcija).
Jebkuram
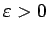 eksistē tāds
eksistē tāds
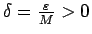 , ka visiem
, ka visiem 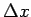 , kuriem
, kuriem
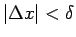 , izpildās nevienādība
, izpildās nevienādība
Tādējādi 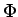 ir nepārtraukta funkcija intervālā
ir nepārtraukta funkcija intervālā ![$ [a;b]$](img524.gif) .
.
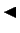
- Sekas.
- Ja
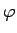 ir nepārtraukta, bet
ir nepārtraukta, bet  ir integrējama
intervālā
ir integrējama
intervālā ![$ [a;b]$](img524.gif) funkcija, tad saskaņā ar teorēmu par saliktas
funkcijas nepārtrauktību
nepārtraukta šajā
intervālā funkcija.
funkcija, tad saskaņā ar teorēmu par saliktas
funkcijas nepārtrauktību
nepārtraukta šajā
intervālā funkcija.
(Pierādīt patstāvīgi.)
- 2. īpašība.
- [Integrāļa ar mainīgu augšējo robežu
diferencēšana]
Ja  ir nepārtraukta intervālā
ir nepārtraukta intervālā ![$ [a;b]$](img524.gif) funkcija, tad
funkcija, tad
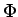 ir
diferencējama šajā intervālā funkcija, pie tam
ir
diferencējama šajā intervālā funkcija, pie tam
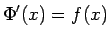
jeb
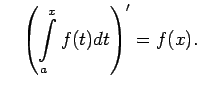
(Integrāļa ar mainīgu augšējo robežu atvasinājums ir vienāds ar zemintegrāļa funkciju,
kas izskaitļota augšējās robežas punktā.)
 Tāpat kā iepriekš, izvēlas patvaļīgu
Tāpat kā iepriekš, izvēlas patvaļīgu
![$ x\in[a;b]$](img664.gif) un
un 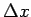 tādu, lai
tādu, lai
![$ x+\Delta x\in[a;b]$](img787.gif) .
.
Apskata
kur
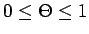 .
.
(Tika pielietota teorēma par noteiktā integrāļa vidējo vērtību.)
Apskata attiecību
Tā kā  ir nepārtraukta funkcija,
tad eksistē robeža šīs vienādības labajai pusei, kad
ir nepārtraukta funkcija,
tad eksistē robeža šīs vienādības labajai pusei, kad
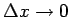 un tā ir vienāda ar
un tā ir vienāda ar 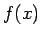 . Tāpēc eksistē arī
robeža šīs vienādības kreisajai pusei, kad
. Tāpēc eksistē arī
robeža šīs vienādības kreisajai pusei, kad
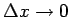 , pie tam
Tādējādi eksistē
, pie tam
Tādējādi eksistē
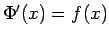 .
.
- Sekas.
- Ja
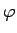 ir diferencējama, bet
ir diferencējama, bet  ir nepārtraukta
intervālā
ir nepārtraukta
intervālā ![$ [a;b]$](img524.gif) funkcija, tad saskaņā ar teorēmu par saliktas
funkcijas diferencēšanu
ir diferencējama šajā intervālā funkcija, pie tam
funkcija, tad saskaņā ar teorēmu par saliktas
funkcijas diferencēšanu
ir diferencējama šajā intervālā funkcija, pie tam
(Pierādīt patstāvīgi.)
-
3.1. piezīme.
- Teorēma par noteiktā integrāļa atvasināšanu pēc
mainīgās augšējās integrēšanas robežas ir viena no matemātiskās
analīzes pamatteorēmām. Šī teorēma izsaka, ka
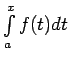 ir viena no intervālā
ir viena no intervālā ![$ [a;b]$](img524.gif) nepārtrauktas
funkcijas primitīvajām funkcijām. Tādējādi jebkurai intervālā
nepārtrauktas
funkcijas primitīvajām funkcijām. Tādējādi jebkurai intervālā
![$ [a;b]$](img524.gif) nepārtrauktai funkcijai eksistē primitīvā funkcija un viena
no tām ir
nepārtrauktai funkcijai eksistē primitīvā funkcija un viena
no tām ir
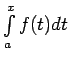 .
.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.2. Sakarība starp noteikto un nenoteikto
Augstāk: 3. INTEGRĀLIS AR MAINĪGU AUGŠĒJO ROBEŽU
Iepriekšējais: 3. INTEGRĀLIS AR MAINĪGU AUGŠĒJO ROBEŽU
2002-11-06
![]() ir intervālā
ir intervālā ![]() integrējama funkcija, tad saskaņā ar
noteiktā integrāļa 2. īpašību tā ir
integrējama katrā no intervāliem
integrējama funkcija, tad saskaņā ar
noteiktā integrāļa 2. īpašību tā ir
integrējama katrā no intervāliem ![]() (
(![]() ), pie tam
šāda integrāļa vērtība ir atkarīga no
), pie tam
šāda integrāļa vērtība ir atkarīga no ![]() .
.
![$\displaystyle \boxed{\int\limits_a^xf(t)dt=\Phi(x),\quad x\in[a;b].}$](img784.gif)
![]() ir intervālā
ir intervālā ![]() integrējama funkcija, tad
integrējama funkcija, tad
![]() ir
nepārtraukta šajā intervālā funkcija.
ir
nepārtraukta šajā intervālā funkcija.
![]() Izvēlas patvaļīgu
Izvēlas patvaļīgu ![]() un patvaļīgu
un patvaļīgu
![]() , bet tādu, lai
, bet tādu, lai
![]() , un apskata
, un apskata
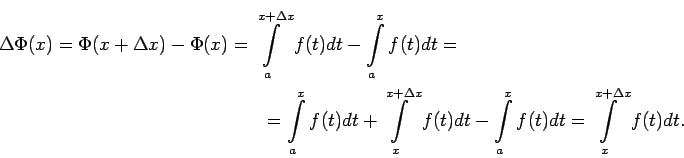
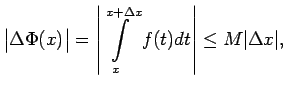
![$ M=\sup\limits_{[a;b]}\vert f(x)\vert$](img790.gif) . (Tāda galīga vērtība eksistē,
jo
. (Tāda galīga vērtība eksistē,
jo 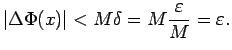
![]() ir nepārtraukta funkcija intervālā
ir nepārtraukta funkcija intervālā ![]() .
.
![]()
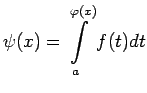
![]() ir nepārtraukta intervālā
ir nepārtraukta intervālā ![]() funkcija, tad
funkcija, tad
![]() ir
diferencējama šajā intervālā funkcija, pie tam
ir
diferencējama šajā intervālā funkcija, pie tam
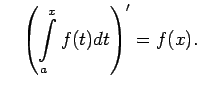
![]() Tāpat kā iepriekš, izvēlas patvaļīgu
Tāpat kā iepriekš, izvēlas patvaļīgu
![]() un
un ![]() tādu, lai
tādu, lai
![]() .
.
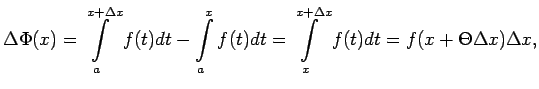
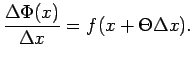
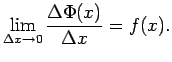
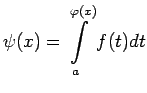
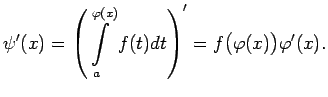
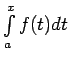 ir viena no intervālā
ir viena no intervālā 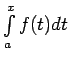 .
.