Matemātika DU TSC
Nākamais: 3.3. Integrēšanas pamatmetodes noteiktajā integrālī Augstāk: 3. INTEGRĀLIS AR MAINĪGU AUGŠĒJO ROBEŽU Iepriekšējais: 3.1. Integrāļa ar mainīgu augšējo robežu

3.2. Sakarība starp noteikto un nenoteikto integrāli

3.1. teorēma. 

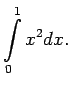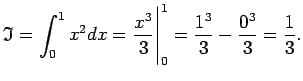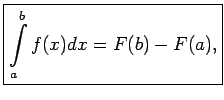
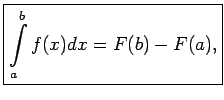
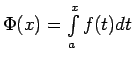Ja $f$ ir nepārtraukta intervālā $[a;b]$ funkcija un $F$ ir viena no $f$ primitīvajām funkcijām šajā intervālā, tad ir spēkā sakarība

$$\boxed{\int\limits_a^bf(x)dx=F(b)-F(a)\/,}$$

kuru sauc par Ņūtona-Leibnica formulu.

(Noteiktais integrālis ir vienāds ar zemintegrāļa funkcijas primitīvās funkcijas pieaugumu intervālā $[a;b]$.)

$\blacktriangleright$ $\Phi(x)=\int\limits_a^xf(t)dt$ ir viena no funkcijas $f$ primitīvajām funkcijām intervālā $[a;b]$. Apzīmē ar $F(x)$ kādu patvaļīgu funkcijas $f$ primitīvo funkciju šajā intervālā.

Tā kā vienas funkcijas divas primitīvās funkcijas var atšķirties tikai par konstanti, tad

$$\int\limits_a^xf(t)dt=F(x)+C\/.$$

Ievieto $x=a$:

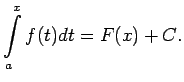
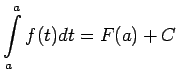$$\int\limits_a^af(t)dt=F(a)+C$$   jeb$$\quad 0=F(a)+C\/.$$

Tādējādi

$$C=-F(a)$$   un$$\quad \int\limits_a^xf(t)dt=F(x)-F(a)\/.$$

Ievieto tagad $x=b$.

$$\int\limits_a^bf(t)dt=F(b)-F(a)\/.\;\blacktriangleleft$$

3.2. piezīme. 

$\phantom{}$

1. Ņūtona-Leibnica formulas labo pusi mēdz apzīmēt ar simbolu $F(x)\left\vert _a^b\right.$ (lasa: funkcija $F(x)$ robežās no $a$ līdz $b$).

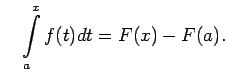
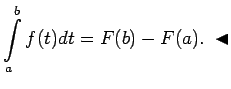
   Ņemot vērā šo apgalvojumu, Ņūtona-Leibnica formulu var pierakstīt šādi:

   $$\int\limits_a^bf(x)dx=F(x)\big\vert _a^b\/.$$

2. Ņūtona-Leibnica formula izsaka sakarību starp noteikto un nenoteikto integrāli, un pēc tās var aprēķināt noteiktā integrāļa vērtību, ja tikai ir zināma kāda no dotās funkcijas primitīvajām funkcijām.

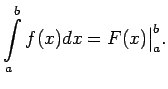
   (Noteiktais integrālis ir skaitlis, pie tam tas nav atkarīgs no tā, kāda no zemintegrāļa funkcijas primitīvajām funkcijām ir izmantota integrāļa aprēķināšanai).

3.1. piemērs. 

Aprēķināt

$$\int\limits_0^1x^2dx\/.$$

$$\mathfrak{I}=\int_0^1x^2dx=\frac{x^3}{3}\Bigg\vert _0^1= \frac{1^3}{3}-\frac{0^3}{3}=\frac{1}{3}\/.$$

Matemātika DU TSC
Nākamais: 3.3. Integrēšanas pamatmetodes noteiktajā integrālī Augstāk: 3. INTEGRĀLIS AR MAINĪGU AUGŠĒJO ROBEŽU Iepriekšējais: 3.1. Integrāļa ar mainīgu augšējo robežu