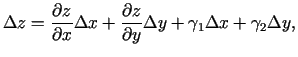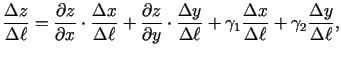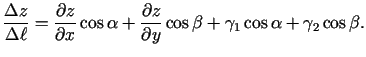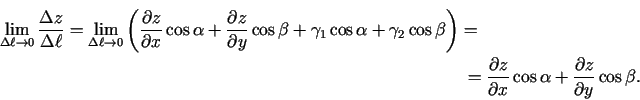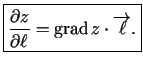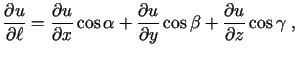Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.7. Augstāku kārtu atvasinājumi
Augstāk: 3. VAIRĀKU ARGUMENTU DIFERENCĒJAMAS FUNKCIJAS
Iepriekšējais: 3.5. Saliktas funkcijas diferencēšana
Apskata punkta
 apkārtnē definētu funkciju
apkārtnē definētu funkciju  un staru
un staru  ar sākumu punktā
ar sākumu punktā  . Uz stara
. Uz stara  punkta
punkta
 apkārtnē izvēlas punktu
apkārtnē izvēlas punktu 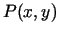 (3.3. zīm.).
(3.3. zīm.).
-
3.5. definīcija.
- Ja attiecībai
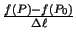 ,
kur
,
kur
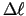 - nogriežņa
- nogriežņa 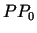 garums, eksistē robeža,
kad
garums, eksistē robeža,
kad
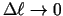 , tad šo robežu sauc par funkcijas
, tad šo robežu sauc par funkcijas
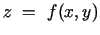 atvasinājumu punktā
atvasinājumu punktā  norādītajā virzienā
norādītajā virzienā 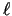 un
apzīmē
un
apzīmē
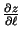 , tādējādi
, tādējādi
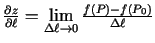 .
.
-
3.6. piezīme.
- Parasti uz stara izvēlas kādu vektoru
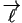 , kura virziens sakrīt ar šī stara virzienu.
, kura virziens sakrīt ar šī stara virzienu.
- Acīmredzami
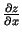 ir funkcijas
ir funkcijas
 atvasinājums
atvasinājums 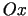 ass pozitīvajā virzienā, bet
ass pozitīvajā virzienā, bet
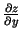 -
- 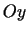 ass pozitīvajā virzienā.
ass pozitīvajā virzienā.
- Atvasinājums
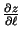 raksturo
funkcijas
raksturo
funkcijas  izmaiņas ātrumu punktā
izmaiņas ātrumu punktā
 virzienā
virzienā
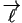 .
.
- Turpmāk var uzskatīt, ka
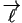 - vienības
vektors, tāpēc tā koordinātas ir
- vienības
vektors, tāpēc tā koordinātas ir
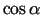 un
un 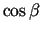 ,
kur
,
kur
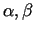 - leņķi, kurus veido
- leņķi, kurus veido
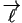 ar
ar
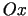 un
un 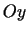 asu pozitīvajiem virzieniem (3.3. zīm.). Acīmredzami
asu pozitīvajiem virzieniem (3.3. zīm.). Acīmredzami
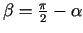 , tāpēc
, tāpēc
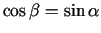 un
un
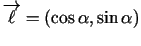 .
.
-
3.6. teorēma.
- Ja funkcijai
 punktā
punktā
 eksistē nepārtraukti parciālie atvasinājumi, tad
tai eksistē šajā punktā atvasinājums
eksistē nepārtraukti parciālie atvasinājumi, tad
tai eksistē šajā punktā atvasinājums
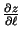 jebkurā virzienā
jebkurā virzienā
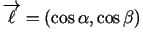 ,
pie tam
,
pie tam
 Saskaņā ar punktā diferencējamas funkcijas
pietiekamo nosacījumu funkcija
Saskaņā ar punktā diferencējamas funkcijas
pietiekamo nosacījumu funkcija  diferencējama punktā
diferencējama punktā
 . Tāpēc
. Tāpēc
kur
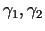 - bezgalīgi mazas
funkcijas, kad
- bezgalīgi mazas
funkcijas, kad
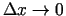 un
un
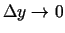 .
Iegūst, ka
kur
.
Iegūst, ka
kur
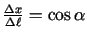 ,
,
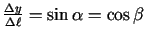 . Tāpēc
Acīmredzami, ja
. Tāpēc
Acīmredzami, ja
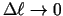 , tad arī
, tad arī
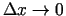 un
un
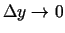 . Tāpēc eksistē
. Tāpēc eksistē
Tādējādi eksistē
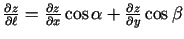 .
.
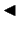
Apskata vektorus
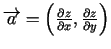 un
un
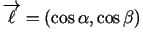 . Šo vektoru
skalārais reizinājums
. Šo vektoru
skalārais reizinājums
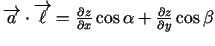 acīmredzami ir
acīmredzami ir
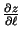 . Tādējādi
. Tādējādi
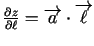 . Šo
vektoru skalāro reizinājumu var uzrakstīt arī citā formā -
vektoriālajā formā:
. Šo
vektoru skalāro reizinājumu var uzrakstīt arī citā formā -
vektoriālajā formā:
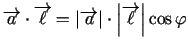 , kur
, kur 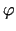 - leņķis starp vektoriem
- leņķis starp vektoriem
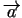 un
un
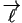 . Šo vektoru skalārais reizinājums sasniedz
maksimālo vērtību, ja
. Šo vektoru skalārais reizinājums sasniedz
maksimālo vērtību, ja
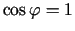 , t.i., ja
, t.i., ja 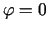 . Seko,
ka funkcijai
. Seko,
ka funkcijai  vislielākais izmaiņas ātrums ir virzienā
vislielākais izmaiņas ātrums ir virzienā
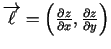 .
.
-
3.6. definīcija.
- Vektoru
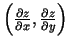 , kas raksturo funkcijas
, kas raksturo funkcijas
 vislielākās izmaiņas ātrumu punktā
vislielākās izmaiņas ātrumu punktā
 , sauc
par šīs funkcijas gradientu3.1 punktā
, sauc
par šīs funkcijas gradientu3.1 punktā  un apzīmē
un apzīmē 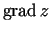 jeb
jeb
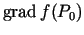 . Tādējādi
. Tādējādi
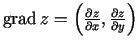 un
un
-
3.7. piezīme.
- Triju argumentu funkcijai
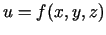 kur
kur
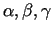 - leņķi atbilstoši ar asīm
- leņķi atbilstoši ar asīm 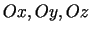 ,
,
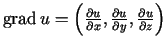 .
.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.7. Augstāku kārtu atvasinājumi
Augstāk: 3. VAIRĀKU ARGUMENTU DIFERENCĒJAMAS FUNKCIJAS
Iepriekšējais: 3.5. Saliktas funkcijas diferencēšana
2002-06-21
![]() apkārtnē definētu funkciju
apkārtnē definētu funkciju ![]() un staru
un staru ![]() ar sākumu punktā
ar sākumu punktā ![]() . Uz stara
. Uz stara ![]() punkta
punkta
![]() apkārtnē izvēlas punktu
apkārtnē izvēlas punktu ![]() (3.3. zīm.).
(3.3. zīm.).

![]() Saskaņā ar punktā diferencējamas funkcijas
pietiekamo nosacījumu funkcija
Saskaņā ar punktā diferencējamas funkcijas
pietiekamo nosacījumu funkcija ![]() diferencējama punktā
diferencējama punktā
![]() . Tāpēc
. Tāpēc