


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.8. Augstāku kārtu diferenciāļi
Augstāk: 3. VAIRĀKU ARGUMENTU DIFERENCĒJAMAS FUNKCIJAS
Iepriekšējais: 3.6. Atvasinājums norādītajā virzienā. Gradients
Apskata kopā  diferencējamu funkciju
diferencējamu funkciju  . Šīs kopas
katrā punktā
. Šīs kopas
katrā punktā 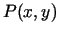 eksistē parciālie atvasinājumi
eksistē parciālie atvasinājumi
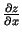 un
un
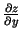 . Šie parciālie atvasinājumi ir kopā
. Šie parciālie atvasinājumi ir kopā  definētas argumentu
definētas argumentu
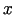 un
un 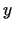 funkcijas, kurām var eksistēt parciālie atvasinājumi,
t.i.,
funkcijas, kurām var eksistēt parciālie atvasinājumi,
t.i.,
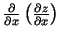 ,
,
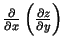 ,
,
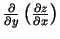 un
un
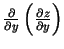 . Ja šie parciālie atvasinājumi (no parciālajiem
atvasinājumiem) eksistē, tad tos sauc par funkcijas
. Ja šie parciālie atvasinājumi (no parciālajiem
atvasinājumiem) eksistē, tad tos sauc par funkcijas  otrās kārtas parciālajiem atvasinājumiem un apzīmē
atbilstoši
otrās kārtas parciālajiem atvasinājumiem un apzīmē
atbilstoši
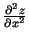 ,
,
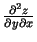 ,
,
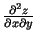 ,
,
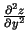 . (Lasa: ``de divi zet pēc
de iks kvadrātā"; ``de divi zet pēc de igrek de iks" utt.). Šos
otrās kārtas parciālos atvasinājumus vēl apzīmē
. (Lasa: ``de divi zet pēc
de iks kvadrātā"; ``de divi zet pēc de igrek de iks" utt.). Šos
otrās kārtas parciālos atvasinājumus vēl apzīmē 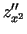 ,
,
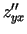 ,
, 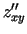 ,
, 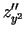 . Tādējādi eksistē četri
funkcijas
. Tādējādi eksistē četri
funkcijas  otrās kārtas parciālie atvasinājumi.
Analoģiski spriežot, var runāt par astoņiem šīs funkcijas trešās
kārtas parciālajiem atvasinājumiem utt.
otrās kārtas parciālie atvasinājumi.
Analoģiski spriežot, var runāt par astoņiem šīs funkcijas trešās
kārtas parciālajiem atvasinājumiem utt.
-
3.7. definīcija.
- Funkcijas parciālos atvasinājumus,
kuriem kārta ir divi un lielāka, sauc par funkcijas augstāku kārtu parciālajiem
atvasinājumiem.
-
3.8. piemērs.
- Atrast funkcijas
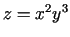 visus otrās kārtas
parciālos atvasinājumus.
visus otrās kārtas
parciālos atvasinājumus.
Atrod
-
3.8. piezīme.
- Šajā piemērā tika iegūts, ka
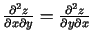 .
Daudzām funkcijām ir spēkā šāda vienādība.
.
Daudzām funkcijām ir spēkā šāda vienādība.
-
3.7. teorēma.
- Ja funkcijai
 punkta
punkta
 apkārtnē eksistē otrās kārtas parciālie atvasinājumi
un tie ir nepārtraukti šajā punktā, tad punktā
apkārtnē eksistē otrās kārtas parciālie atvasinājumi
un tie ir nepārtraukti šajā punktā, tad punktā
 izpildās sakarība
izpildās sakarība
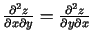 .
.
 Izvēlas tādus argumentu patvaļīgus pieaugumus
Izvēlas tādus argumentu patvaļīgus pieaugumus
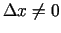 un
un
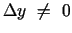 , ka punkts
, ka punkts
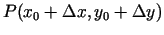 pieder punkta
pieder punkta
 apkārtnei
(3.4. zīm.).
apkārtnei
(3.4. zīm.).
Apskata
Izveido funkciju
Tā kā funkcijai  punkta
punkta
 apkārtnē eksistē
atvasinājums
apkārtnē eksistē
atvasinājums
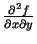 , tad
funkcijai
, tad
funkcijai
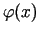 eksistē atvasinājums intervālā
eksistē atvasinājums intervālā
![$ [x_0,x_0+\Delta x]$](img569.gif) un
un
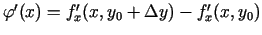 .
.
Tā kā
un
tad
Šai starpībai pielieto Lagranža formulu intervālā
![$ \;[x_0,x_0+\Delta x]\;$](img574.gif) . Iegūst
. Iegūst
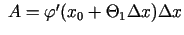 , kur
, kur
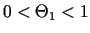 jeb
Starpībai pielieto Lagranža formulu intervālā
jeb
Starpībai pielieto Lagranža formulu intervālā
![$ [y_0,y_0+\Delta y]$](img578.gif)
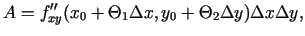 |
(3.6) |
kur
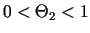 (funkcijai
(funkcijai  punkta
punkta
 apkārtnē
eksistē parciālais atvasinājums
apkārtnē
eksistē parciālais atvasinājums 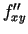 ).
).
Ja izveidotu otru funkciju
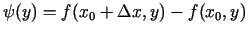 un
rīkotos analoģiski, tad iegūtu, ka
un
rīkotos analoģiski, tad iegūtu, ka
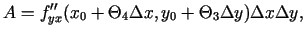 |
(3.7) |
kur
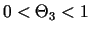 un arī
un arī
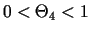 . No vienādībām
(3.6), (3.7) seko:
Vienādības abas puses izdala ar
. No vienādībām
(3.6), (3.7) seko:
Vienādības abas puses izdala ar
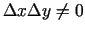 .
Šajā
vienādībā pāriet pie robežas, kad
.
Šajā
vienādībā pāriet pie robežas, kad
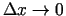 un
un
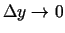 (robežas punktā
(robežas punktā
 eksistē, jo parciālie
atvasinājumi
eksistē, jo parciālie
atvasinājumi 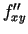 un
un 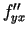 ir nepārtrauktas šajā punktā
funkcijas). Iegūst
ir nepārtrauktas šajā punktā
funkcijas). Iegūst
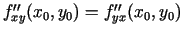 .
.
-
3.9. piezīme.
- Analoģiska teorēma ir spēkā arī
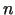 argumentu
funkcijai. Nepārtrauktie
argumentu
funkcijai. Nepārtrauktie 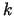 - tās kārtas parciālie atvasinājumi
vienādi, ja pēc katra no mainīgajiem atvasināts tikpat daudz reižu.
- tās kārtas parciālie atvasinājumi
vienādi, ja pēc katra no mainīgajiem atvasināts tikpat daudz reižu.
Piemēram,
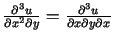 , kur
, kur
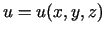 un parciālie atvasinājumi ir nepārtraukti.
un parciālie atvasinājumi ir nepārtraukti.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.8. Augstāku kārtu diferenciāļi
Augstāk: 3. VAIRĀKU ARGUMENTU DIFERENCĒJAMAS FUNKCIJAS
Iepriekšējais: 3.6. Atvasinājums norādītajā virzienā. Gradients
2002-06-21
![]() diferencējamu funkciju
diferencējamu funkciju ![]() . Šīs kopas
katrā punktā
. Šīs kopas
katrā punktā ![]() eksistē parciālie atvasinājumi
eksistē parciālie atvasinājumi
![]() un
un
![]() . Šie parciālie atvasinājumi ir kopā
. Šie parciālie atvasinājumi ir kopā ![]() definētas argumentu
definētas argumentu
![]() un
un ![]() funkcijas, kurām var eksistēt parciālie atvasinājumi,
t.i.,
funkcijas, kurām var eksistēt parciālie atvasinājumi,
t.i.,
![]() ,
,
![]() ,
,
![]() un
un
![]() . Ja šie parciālie atvasinājumi (no parciālajiem
atvasinājumiem) eksistē, tad tos sauc par funkcijas
. Ja šie parciālie atvasinājumi (no parciālajiem
atvasinājumiem) eksistē, tad tos sauc par funkcijas ![]() otrās kārtas parciālajiem atvasinājumiem un apzīmē
atbilstoši
otrās kārtas parciālajiem atvasinājumiem un apzīmē
atbilstoši
![]() ,
,
![]() ,
,
![]() ,
,
![]() . (Lasa: ``de divi zet pēc
de iks kvadrātā"; ``de divi zet pēc de igrek de iks" utt.). Šos
otrās kārtas parciālos atvasinājumus vēl apzīmē
. (Lasa: ``de divi zet pēc
de iks kvadrātā"; ``de divi zet pēc de igrek de iks" utt.). Šos
otrās kārtas parciālos atvasinājumus vēl apzīmē ![]() ,
,
![]() ,
, ![]() ,
, ![]() . Tādējādi eksistē četri
funkcijas
. Tādējādi eksistē četri
funkcijas ![]() otrās kārtas parciālie atvasinājumi.
Analoģiski spriežot, var runāt par astoņiem šīs funkcijas trešās
kārtas parciālajiem atvasinājumiem utt.
otrās kārtas parciālie atvasinājumi.
Analoģiski spriežot, var runāt par astoņiem šīs funkcijas trešās
kārtas parciālajiem atvasinājumiem utt.
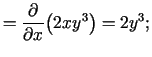
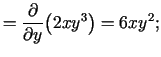
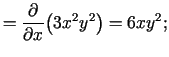
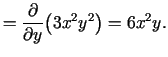
![]() Izvēlas tādus argumentu patvaļīgus pieaugumus
Izvēlas tādus argumentu patvaļīgus pieaugumus
![]() un
un
![]() , ka punkts
, ka punkts
![]() pieder punkta
pieder punkta
![]() apkārtnei
(3.4. zīm.).
apkārtnei
(3.4. zīm.).
![]() , kur
, kur
![]() un parciālie atvasinājumi ir nepārtraukti.
un parciālie atvasinājumi ir nepārtraukti.