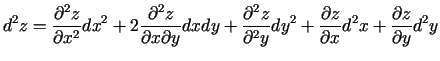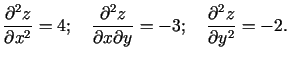Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.9. Teilora formula divu argumentu funkcijai
Augstāk: 3. VAIRĀKU ARGUMENTU DIFERENCĒJAMAS FUNKCIJAS
Iepriekšējais: 3.7. Augstāku kārtu atvasinājumi
Apskata kopā  diferencējamu funkciju
diferencējamu funkciju  . Par šādas
funkcijas diferenciāli sauc
. Par šādas
funkcijas diferenciāli sauc
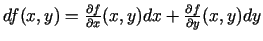 . Ja
. Ja
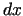 un
un 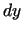 ir fiksēti, tad
ir fiksēti, tad 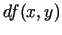 var uzskatīt par mainīgo
var uzskatīt par mainīgo
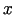 un
un 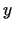 funkciju. Pie tam, ja šī funkcija ir diferencējama, tad
var runāt par tās diferenciāli, t.i.,
funkciju. Pie tam, ja šī funkcija ir diferencējama, tad
var runāt par tās diferenciāli, t.i.,
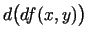 , kuru
attiecībā pret
, kuru
attiecībā pret  sauc par otrās kārtas
diferenciāli un apzīmē
sauc par otrās kārtas
diferenciāli un apzīmē 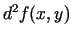 . Tātad
. Tātad
(Izmantoja, ka
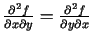 ).
).
Analoģiski definē 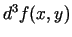 un vispārīgi
un vispārīgi
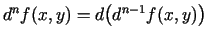 . Simboliski var rakstīt
. Simboliski var rakstīt
Analoģiski var apskatīt augstāku kārtu diferenciāļus 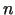 argumentu
funkcijai.
argumentu
funkcijai.
-
3.10. piezīme.
- Ja
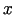 un
un 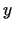 nav neatkarīgie argumenti, bet
starpargumenti, t.i.,
nav neatkarīgie argumenti, bet
starpargumenti, t.i.,  , kur
, kur 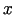 un
un 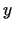 ir viena vai
vairāku neatkarīgo argumentu funkcijas, tad, piemēram,
utt.
ir viena vai
vairāku neatkarīgo argumentu funkcijas, tad, piemēram,
utt.
-
3.9. piemērs.
- Atrast funkcijas
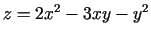 otrās kārtas
diferenciāli.
otrās kārtas
diferenciāli.
Atrod
Tādējādi



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.9. Teilora formula divu argumentu funkcijai
Augstāk: 3. VAIRĀKU ARGUMENTU DIFERENCĒJAMAS FUNKCIJAS
Iepriekšējais: 3.7. Augstāku kārtu atvasinājumi
2002-06-21
![]() diferencējamu funkciju
diferencējamu funkciju ![]() . Par šādas
funkcijas diferenciāli sauc
. Par šādas
funkcijas diferenciāli sauc
![]() . Ja
. Ja
![]() un
un ![]() ir fiksēti, tad
ir fiksēti, tad ![]() var uzskatīt par mainīgo
var uzskatīt par mainīgo
![]() un
un ![]() funkciju. Pie tam, ja šī funkcija ir diferencējama, tad
var runāt par tās diferenciāli, t.i.,
funkciju. Pie tam, ja šī funkcija ir diferencējama, tad
var runāt par tās diferenciāli, t.i.,
![]() , kuru
attiecībā pret
, kuru
attiecībā pret ![]() sauc par otrās kārtas
diferenciāli un apzīmē
sauc par otrās kārtas
diferenciāli un apzīmē ![]() . Tātad
. Tātad
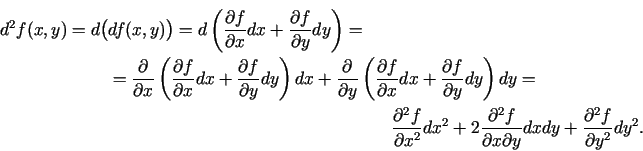
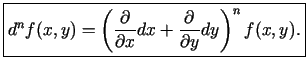
![]() argumentu
funkcijai.
argumentu
funkcijai.