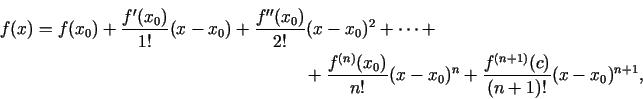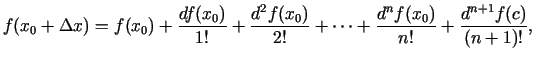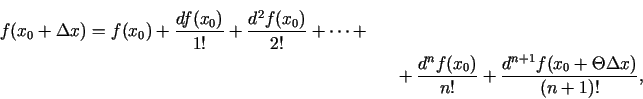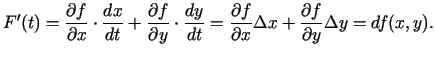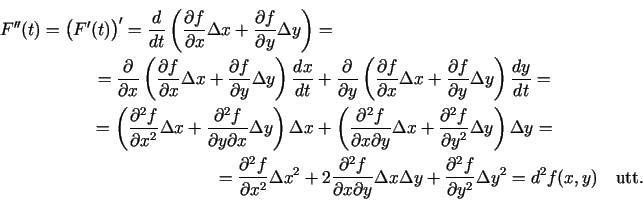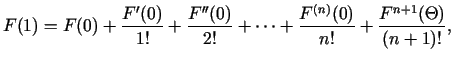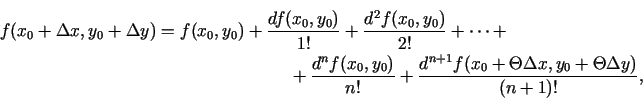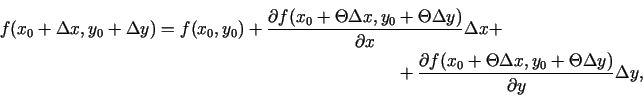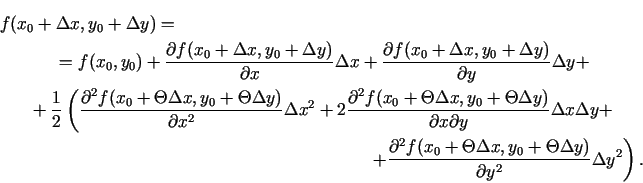Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.10. Jautājumi
Augstāk: 3. VAIRĀKU ARGUMENTU DIFERENCĒJAMAS FUNKCIJAS
Iepriekšējais: 3.8. Augstāku kārtu diferenciāļi
Teilora formulu divu argumentu funkcijai var iegūt, izmantojot
Teilora formulu viena argumenta funkcijai. Ja funkcijai 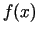 punkta
punkta
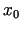 apkārtnē eksistē visi atvasinājumi līdz
apkārtnē eksistē visi atvasinājumi līdz 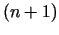 kārtai
ieskaitot, tad visiem
kārtai
ieskaitot, tad visiem 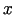 , kas pieder šai apkārtnei, ir spēkā
vienādība
, kas pieder šai apkārtnei, ir spēkā
vienādība
kur
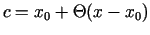 un
un
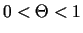 . Ja apzīmē
. Ja apzīmē
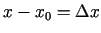 un izmanto funkcijas
un izmanto funkcijas 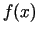 diferenciāļu aprēķināšanas formulas, tad
Teilora formulu var uzrakstīt šādi:
diferenciāļu aprēķināšanas formulas, tad
Teilora formulu var uzrakstīt šādi:
kur
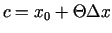 un
un
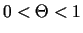 jeb
jeb
kur
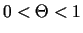 .
.
Tagad apskata funkciju  , kurai punkta
, kurai punkta  apkārtnē
eksistē visi diferenciāļi līdz
apkārtnē
eksistē visi diferenciāļi līdz 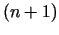 kārtai ieskaitot.
kārtai ieskaitot.
Izvēlas tādus patvaļīgus argumentu pieaugumus 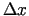 un
un
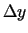 , lai punkts
, lai punkts
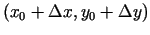 piederētu
šai apkārtnei. Apskata
piederētu
šai apkārtnei. Apskata
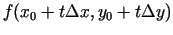 , kur
, kur
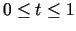 . Šo izteiksmi fiksētiem
. Šo izteiksmi fiksētiem 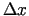 un
un 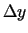 var uzskatīt par mainīgā
var uzskatīt par mainīgā 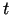 funkciju
funkciju 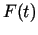 . Tādējādi
. Tādējādi
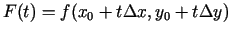 , kur
, kur
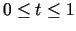 .
Funkcijai
.
Funkcijai 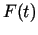 intervālā
intervālā ![$ [0,1]$](img618.gif) eksistē visi atvasinājumi līdz
eksistē visi atvasinājumi līdz
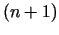 kārtai ieskaitot. Tiešām, ja
kārtai ieskaitot. Tiešām, ja 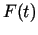 uzskata par saliktu
funkciju
uzskata par saliktu
funkciju
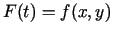 , kur
, kur
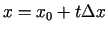 ,
,
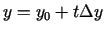 ,
tad
,
tad 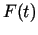 ir diferencējama funkcija kā salikta funkcija, pie tam
Funkcija
ir diferencējama funkcija kā salikta funkcija, pie tam
Funkcija 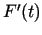 arī ir diferencējama.
(Pamatot patstāvīgi!)
arī ir diferencējama.
(Pamatot patstāvīgi!)
Tāpēc eksistē
Beidzot, eksistē
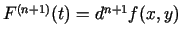 .
.
Funkcijai 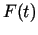 uzraksta Teilora formulu (izvēlas
uzraksta Teilora formulu (izvēlas 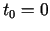 un
un
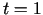 ):
kur
):
kur
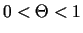 . Funkcijas
. Funkcijas
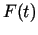 un tās atvasinājumu vērtības aizstāj ar
atbilstošajām izteiksmēm. Iegūst, ka
un tās atvasinājumu vērtības aizstāj ar
atbilstošajām izteiksmēm. Iegūst, ka
kur
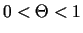 .
.
Iegūtā formula ir funkcijas  Teilora formula
punkta
Teilora formula
punkta  apkārtnē.
apkārtnē.
Ja 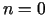 , tad iegūst Teilora formulas atsevišķo gadījumu - Lagranža
formulu:
jeb
, tad iegūst Teilora formulas atsevišķo gadījumu - Lagranža
formulu:
jeb
kur
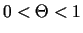 .
.
Ja 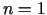 , tad iegūst
, tad iegūst



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.10. Jautājumi
Augstāk: 3. VAIRĀKU ARGUMENTU DIFERENCĒJAMAS FUNKCIJAS
Iepriekšējais: 3.8. Augstāku kārtu diferenciāļi
2002-06-21
![]() punkta
punkta
![]() apkārtnē eksistē visi atvasinājumi līdz
apkārtnē eksistē visi atvasinājumi līdz ![]() kārtai
ieskaitot, tad visiem
kārtai
ieskaitot, tad visiem ![]() , kas pieder šai apkārtnei, ir spēkā
vienādība
, kas pieder šai apkārtnei, ir spēkā
vienādība