


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.11. Vingrinājumi
Augstāk: 3. VAIRĀKU ARGUMENTU DIFERENCĒJAMAS FUNKCIJAS
Iepriekšējais: 3.9. Teilora formula divu argumentu funkcijai
- Definēt punktā diferencējamu funkciju un tās diferenciāli
šajā punktā.
- Formulēt punktā diferencējamas funkcijas nepieciešamos
nosacījumus.
- Definēt funkcijas parciālos atvasinājumus un sniegt tiem
ģeometrisko interpretāciju.
- Formulēt punktā diferencējamas funkcijas pietiekamo
nosacījumu.
- Paskaidrot, kā lieto diferenciāli, lai aprēķinātu
tuvinātu funkcijas vērtību.
- Definēt funkcijas
 grafika pieskarplakni un normāli.
grafika pieskarplakni un normāli.
- Uzrakstīt funkcijas
 grafika pieskarplaknes un
normāles vienādojumus.
grafika pieskarplaknes un
normāles vienādojumus.
- Kādai ir jābūt funkcijai
 , lai tās grafikam eksistētu
pieskarplakne.
, lai tās grafikam eksistētu
pieskarplakne.
- Formulēt teorēmu par saliktas funkcijas diferencēšanu.
- Definēt funkcijas
 atvasinājumu norādītajā virzienā.
atvasinājumu norādītajā virzienā.
- Uzrakstīt funkcijai
 atvasinājuma norādītajā virzienā
atrašanas formulu.
atvasinājuma norādītajā virzienā
atrašanas formulu.
- Kāds sakars pastāv starp funkcijas parciālajiem
atvasinājumiem un atvasinājumu norādītajā virzienā?
- Definēt divu argumentu funkcijas gradientu.
- Uzrakstīt formulu, kas saista funkcijas atvasinājumu
norādītajā virzienā ar funkcijas gradientu.
- Definēt divu argumentu funkcijas otrās kārtas parciālos
atvasinājumus.
- Definēt triju argumentu funkcijas
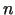 - tās kārtas parciālos
atvasinājumus.
- tās kārtas parciālos
atvasinājumus.
- Formulēt tos nosacījumus, kad parciālie atvasinājumi nav
atkarīgi no atvasināšanas secības.
- Definēt otrās kārtas diferenciāli divu argumentu funkcijai.
- Uzrakstīt
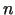 - tās kārtas diferenciāļa aprēķināšanas
simbolisko formulu un paskaidrot tās pielietošanu.
- tās kārtas diferenciāļa aprēķināšanas
simbolisko formulu un paskaidrot tās pielietošanu.
- Uzrakstīt Teilora formulu divu un triju argumentu funkcijām.
- Paskaidrot, kā Teilora formulu var pielietot funkcijas aptuveno
vērtību izskaitļošanā.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.11. Vingrinājumi
Augstāk: 3. VAIRĀKU ARGUMENTU DIFERENCĒJAMAS FUNKCIJAS
Iepriekšējais: 3.9. Teilora formula divu argumentu funkcijai
2002-06-21