


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4. VAIRĀKU ARGUMENTU FUNKCIJU PĒTĪŠANA UZ
Augstāk: 3. VAIRĀKU ARGUMENTU DIFERENCĒJAMAS FUNKCIJAS
Iepriekšējais: 3.10. Jautājumi
- Definēt punktā
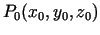 diferencējamu funkciju
diferencējamu funkciju
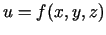 un tās diferenciāli šajā punktā.
un tās diferenciāli šajā punktā.
- Pierādīt, ka punktā diferencējamai funkcijai
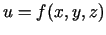 eksistē parciālie atvasinājumi un tā ir nepārtraukta funkcija šajā
punktā.
eksistē parciālie atvasinājumi un tā ir nepārtraukta funkcija šajā
punktā.
- Atrast funkciju parciālos atvasinājumus
a)
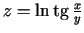 ;
;
b)
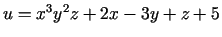 .
.
- Pierādīt, ka funkcija
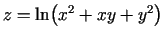 apmierina
nosacījumu
apmierina
nosacījumu
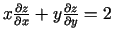 .
.
- Izskaitļot
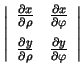 , ja
, ja
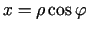 un
un
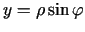 .
.
- Pierādīt, ka funkcijai
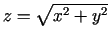 punktā
punktā  neeksistē parciālie atvasinājumi.
neeksistē parciālie atvasinājumi.
- Atrast funkciju
 , ja
, ja
a)
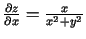 ;
;
b)
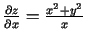 un
un
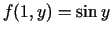 .
.
c)
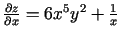 un
un
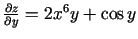 .
.
- Caur virsmas
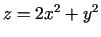 punktu
punktu 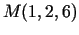 konstruētas divas
plaknes, kas paralēlas koordinātu plaknēm
konstruētas divas
plaknes, kas paralēlas koordinātu plaknēm 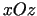 un
un 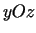 . Aprēķināt
leņķus, kādus veido punktā
. Aprēķināt
leņķus, kādus veido punktā 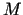 konstruētās pieskares līnijām, pa
kurām šīs plaknes šķeļ virsmu, ar atbilstošajām koordinātu asīm.
konstruētās pieskares līnijām, pa
kurām šīs plaknes šķeļ virsmu, ar atbilstošajām koordinātu asīm.
- Atrast funkcijas
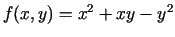 pilno pieaugumu un
diferenciāli.
pilno pieaugumu un
diferenciāli.
- Funkcijai
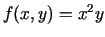 atrast pilno pieaugumu un
diferenciāli punktā
atrast pilno pieaugumu un
diferenciāli punktā 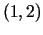 . Iegūtos rezultātus salīdzināt, ja
. Iegūtos rezultātus salīdzināt, ja
a)
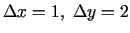 ;
;
b)
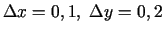 ;
;
c)
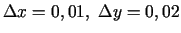 .
.
- Pierādīt, ka funkcijām
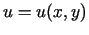 un
un 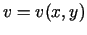 izpildās
izpildās
a)
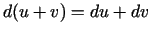 ;
;
b)
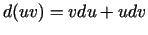 ;
;
c)
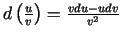 .
.
- Atrast
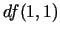 , ja
, ja
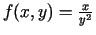 .
.
- Atrast
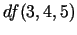 , ja
, ja
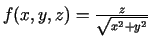 .
.
- Sniegt ģeometrisko interpretāciju funkcijas
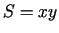 pilnajam
pieaugumam un diferenciālim. (Apskatīt taisnstūri, kura malas ir
pilnajam
pieaugumam un diferenciālim. (Apskatīt taisnstūri, kura malas ir 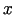 un
un
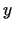 ).
).
- Uzrakstīt aptuveno vienādību triju argumentu funkcijas
vērtību izskaitļošanai.
- Noslēgta kaste, kuras ārējie izmēri ir
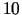 cm,
cm, 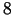 cm un
cm un 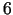 cm,
izgatavota no skārda, kura biezums
cm,
izgatavota no skārda, kura biezums 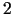 mm. Aprēķināt tuvinātu
patērētā metāla tilpuma vērtību.
mm. Aprēķināt tuvinātu
patērētā metāla tilpuma vērtību.
- Tuvināti izskaitļot
a)
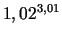 ;
;
b)
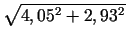 .
.
-
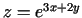 , kur
, kur 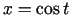 ,
, 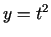 . Atrast
. Atrast
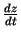 .
.
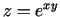 , kur
, kur 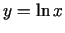 . Atrast
. Atrast
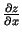 un
un
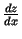 .
.
- Parādīt, ka funkcija
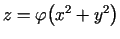 apmierina vienādojumu
apmierina vienādojumu
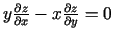 .
.
-
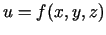 , kur
, kur
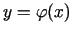 ,
,
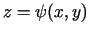 . Atrast
. Atrast
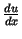 .
.
- Atrast funkcijas
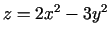 atvasinājumu punktā
atvasinājumu punktā
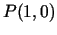 virzienā, kas veido ar
virzienā, kas veido ar 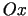 asi leņki
asi leņki
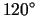 .
.
- Atrast funkcijas
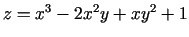 atvasinājumu punktā
atvasinājumu punktā
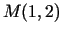 virzienā no šī punkta uz punktu
virzienā no šī punkta uz punktu 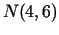 .
.
- Atrast funkcijas
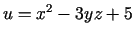 atvasinājumu punktā
atvasinājumu punktā
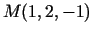 virzienā, kas veido ar koordinātu asīm vienādus
leņķus.
virzienā, kas veido ar koordinātu asīm vienādus
leņķus.
- Atrast un ilustrēt ģeometriski funkcijas
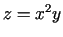 gradientu punktā
gradientu punktā 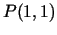 .
.
- Atrast funkcijas
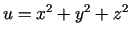 gradienta punktā
gradienta punktā
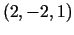 moduli un virzienu.
moduli un virzienu.
- Atrast leņķi starp funkcijas
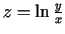 gradientiem punktos
gradientiem punktos
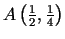 un
un
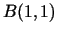 .
.
- Atrast funkcijas
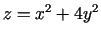 vislielāko izmaiņas ātrumu
punktā
vislielāko izmaiņas ātrumu
punktā 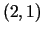 .
.
- Atrast funkcijas
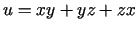 visus otrās kārtas parciālos
atvasinājumus.
visus otrās kārtas parciālos
atvasinājumus.
- Parādīt, ka funkcijai
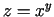 izpildās
izpildās
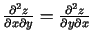 .
.
- Atrast
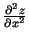 ,
,
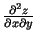 ,
,
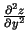 , ja
, ja 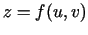 , kur
, kur 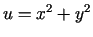 ,
, 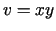 .
.
- Atrast
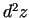 , ja
, ja 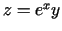 .
.
- Uzrakstīt funkcijas
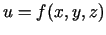 otrās kārtas diferenciāļa
aprēķināšanas formulas (apskatīt gadījumu, kad
otrās kārtas diferenciāļa
aprēķināšanas formulas (apskatīt gadījumu, kad 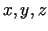 - neatkarīgie
argumenti, un gadījumu, kad
- neatkarīgie
argumenti, un gadījumu, kad 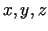 - starpargumenti).
- starpargumenti).
- Atrast
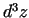 , ja
, ja
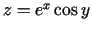 .
.
- Funkcijai
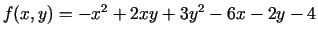 uzrakstīt Teilora
formulu punkta
uzrakstīt Teilora
formulu punkta 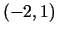 apkārtnē.
apkārtnē.
- Funkcijai
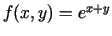 uzrakstīt Teilora formulu
punkta
uzrakstīt Teilora formulu
punkta 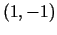 apkārtnē. Iegūt arī atsevišķus gadījumus, kad
apkārtnē. Iegūt arī atsevišķus gadījumus, kad
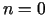 un
un 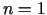 .
.
- Izmantojot Teilora formulu, tuvināti izskaitļot
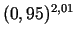 . Aprēķinos izmantot tikai tos formulas locekļus,
kas pēc moduļa nav mazāki par
. Aprēķinos izmantot tikai tos formulas locekļus,
kas pēc moduļa nav mazāki par 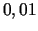 .
.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4. VAIRĀKU ARGUMENTU FUNKCIJU PĒTĪŠANA UZ
Augstāk: 3. VAIRĀKU ARGUMENTU DIFERENCĒJAMAS FUNKCIJAS
Iepriekšējais: 3.10. Jautājumi
2002-06-21
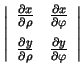 , ja
, ja
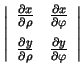 , ja
, ja