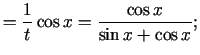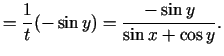Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.6. Atvasinājums norādītajā virzienā. Gradients
Augstāk: 3. VAIRĀKU ARGUMENTU DIFERENCĒJAMAS FUNKCIJAS
Iepriekšējais: 3.4. Pieskarplakne
-
3.5. teorēma.
- Ja kopā
 definēta salikta funkcija
definēta salikta funkcija 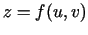 ,
kur
,
kur
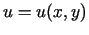 ,
, 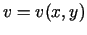 , funkcijām
, funkcijām 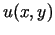 ,
, 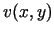 punkta
punkta
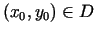 apkārtnē eksistē nepārtraukti parciālie atvasinājumi un
funkcijai
apkārtnē eksistē nepārtraukti parciālie atvasinājumi un
funkcijai
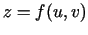 atbilstoša punkta
atbilstoša punkta 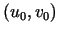 apkārtnē eksistē
nepārtraukti parciālie atvasinājumi, tad
salikta
funkcija
apkārtnē eksistē
nepārtraukti parciālie atvasinājumi, tad
salikta
funkcija
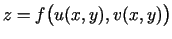 ir diferencējama punktā
ir diferencējama punktā  ,
pie tam
,
pie tam
 Tā kā funkcijām
Tā kā funkcijām 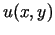 ,
, 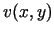 punkta
punkta
 apkārtnē eksistē nepārtraukti parciālie atvasinājumi, tad
funkcijas ir diferencējamas šajā punktā, t.i.,
apkārtnē eksistē nepārtraukti parciālie atvasinājumi, tad
funkcijas ir diferencējamas šajā punktā, t.i.,
un
kur 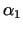 ,
,
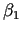 ,
, 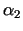 ,
, 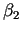 - bezgalīgi mazas funkcijas, kad
- bezgalīgi mazas funkcijas, kad
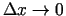 un
un
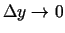 .
.
Ja uzskata, ka
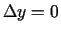 , tad iegūst šo funkciju parciālos
pieaugumus.
, tad iegūst šo funkciju parciālos
pieaugumus.
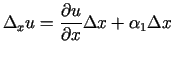 un un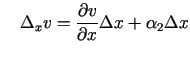 |
(3.4) |
Šiem pieaugumiem atbilst funkcijas 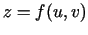 pieaugums, kuru ir
lietderīgi apzīmēt
pieaugums, kuru ir
lietderīgi apzīmēt
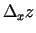 .
.
Tā kā funkcijai 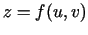 punkta
punkta 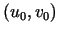 apkārtnē eksistē
nepārtraukti parciālie atvasinājumi, tad tā ir diferencējama šajā
punktā.
apkārtnē eksistē
nepārtraukti parciālie atvasinājumi, tad tā ir diferencējama šajā
punktā.
Tāpēc
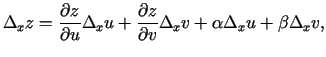 |
(3.5) |
kur
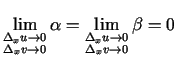 .
.
Vienādībā (3.5)
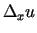 un
un
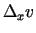 aizstāj ar
atbilstošajām izteiksmēm (3.4)
aizstāj ar
atbilstošajām izteiksmēm (3.4)
kur
ir bezgalīgi maza funkcija, kad
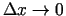 (
(
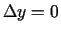 ).
).
Atrod
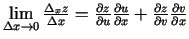 .
Tādējādi eksistē
.
Tādējādi eksistē
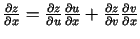 , kas acīmredzami ir
nepārtraukts punkta
, kas acīmredzami ir
nepārtraukts punkta  apkārtnē. Analoģiski pierāda, ka šī
punkta apkārtnē eksistē nepārtraukts
apkārtnē. Analoģiski pierāda, ka šī
punkta apkārtnē eksistē nepārtraukts
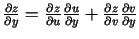 .
Saskaņā ar funkcijas diferencējamības pietiekamo nosacījumu
(3.3. teorēma) funkcija
.
Saskaņā ar funkcijas diferencējamības pietiekamo nosacījumu
(3.3. teorēma) funkcija
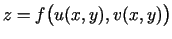 diferencējama punktā
diferencējama punktā  .
.
-
3.6. piemērs.
- Atrast funkcijas
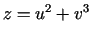 , kur
, kur
![$ u=\sqrt[3]{xy}$](img468.gif) ,
,
![$ v=\sqrt[5]{\frac{x}{y}}$](img469.gif) , parciālos atvasinājumus
, parciālos atvasinājumus
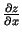 un
un
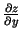 .
.
Atrod
Tādējādi
kur
![$ u=\sqrt[3]{xy}$](img468.gif) ,
,
![$ v=\sqrt[5]{\frac{x}{y}}$](img469.gif) .
.
-
3.7. piemērs.
- Atrast funkcijas
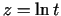 , kur
, kur
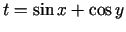 ,
parciālos atvasinājumus
,
parciālos atvasinājumus
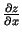 ,
,
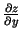 .
.
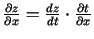 ;
;
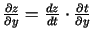 . Atrod
. Atrod
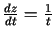 ;
;
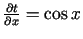 ,
,
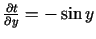 .
.
Tādējādi



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.6. Atvasinājums norādītajā virzienā. Gradients
Augstāk: 3. VAIRĀKU ARGUMENTU DIFERENCĒJAMAS FUNKCIJAS
Iepriekšējais: 3.4. Pieskarplakne
2002-06-21
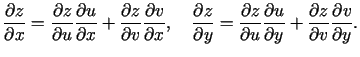
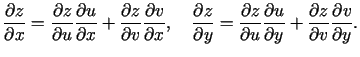
![]() Tā kā funkcijām
Tā kā funkcijām ![]() ,
, ![]() punkta
punkta
![]() apkārtnē eksistē nepārtraukti parciālie atvasinājumi, tad
funkcijas ir diferencējamas šajā punktā, t.i.,
apkārtnē eksistē nepārtraukti parciālie atvasinājumi, tad
funkcijas ir diferencējamas šajā punktā, t.i.,
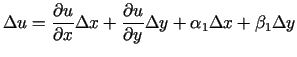
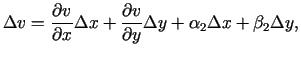
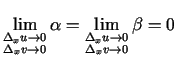 .
.
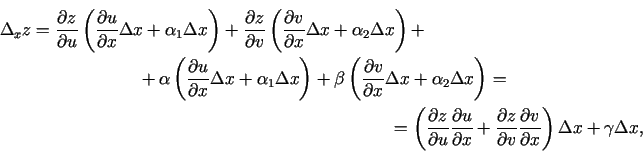
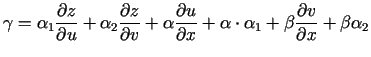
![$\displaystyle =\sqrt[3]{y}\cdot\frac{1}{3\sqrt[3]{x^2}},$](img474.gif)
![$\displaystyle =\sqrt[3]{x}\cdot\frac{1}{3\sqrt[3]{y^2}},$](img475.gif)
![$\displaystyle =\frac{1}{\sqrt[5]{y}}\cdot\frac{1}{5\sqrt[5]{x^4}},$](img477.gif)
![$\displaystyle =\sqrt[5]{x}\left(y^{-\frac{1}{5}}\right)_y'=-\frac{1}{5}\sqrt[5]{x}\cdot\frac{1}{\sqrt[5]{y^6}}\/.$](img479.gif)
![$\displaystyle \frac{\partial z}{\partial
x}=\frac{2u}{3}\cdot\sqrt[3]{\frac{y}{...
...{3}\cdot\sqrt[3]{\frac{x}{y^2}}-\frac{3v^2}{5}\cdot{\sqrt[5]{\frac{x}{y^6}}}\/,$](img480.gif)