Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.5. Saliktas funkcijas diferencēšana
Augstāk: 3. VAIRĀKU ARGUMENTU DIFERENCĒJAMAS FUNKCIJAS
Iepriekšējais: 3.3. Funkcijas diferenciāļa lietojumi tuvinātos aprēķinos
Apskata funkciju  , kas ir nepārtraukta punktā
, kas ir nepārtraukta punktā
 .
.
-
3.3. definīcija.
- Par funkcijas grafika pieskarplakni
punktā
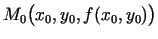 sauc plakni, kas iet
caur šo punktu un kas apmierina šādu nosacījumu: attālums
sauc plakni, kas iet
caur šo punktu un kas apmierina šādu nosacījumu: attālums 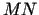 no grafika patvaļīga punkta
no grafika patvaļīga punkta
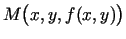 līdz šai
plaknei ir pēc patikas mazs, salīdzinot ar attālumu
līdz šai
plaknei ir pēc patikas mazs, salīdzinot ar attālumu 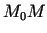 , kad
, kad
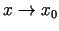 un
un
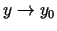 , citiem vārdiem,
, citiem vārdiem,
![$ \frac{MN}{M_0M}
\xrightarrow[\substack{x\rightarrow x_0\\ y\rightarrow y_0}]{\/}0$](img417.gif) (skat. 3.2. zīm.).
(skat. 3.2. zīm.).
-
3.4. teorēma.
- Ja funkcija
 ir diferencējama
punktā
ir diferencējama
punktā
 , tad tās grafikam atbilstošajā punktā
, tad tās grafikam atbilstošajā punktā
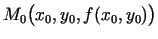 eksistē pieskarplakne, kuras vienādojums ir
eksistē pieskarplakne, kuras vienādojums ir
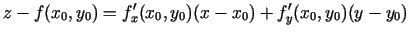 |
(3.1) |
 Tā kā funkcija
Tā kā funkcija  ir diferencējama punktā
ir diferencējama punktā
 , tad tā ir nepārtraukta šajā punktā un izpildās
sakarība
, tad tā ir nepārtraukta šajā punktā un izpildās
sakarība
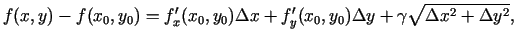 |
(3.2) |
kur
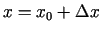 ,
,
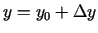 un
un
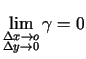 . Acīmredzami (3.1) ir plaknes, kas iet caur
punktu
. Acīmredzami (3.1) ir plaknes, kas iet caur
punktu
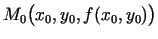 , vienādojums. Atliek
pierādīt, ka šī plakne ir funkcijas
, vienādojums. Atliek
pierādīt, ka šī plakne ir funkcijas  grafikam punktā
grafikam punktā 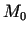 konstruētā pieskarplakne. Tam nolūkam ir jāparāda, ka
konstruētā pieskarplakne. Tam nolūkam ir jāparāda, ka
![$ \frac{MN}{M_0M}
\xrightarrow[\substack{x\rightarrow x_0\\ y\rightarrow y_0}]{\/}0$](img417.gif) (3.2. zīm.). No vienādības (3.2) atņem (3.1) un iegūst
(3.2. zīm.). No vienādības (3.2) atņem (3.1) un iegūst
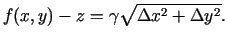 |
(3.3) |
Apskata attiecību
kur
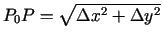 . Var saskatīt, ka
. Var saskatīt, ka
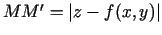 (situācijā, kas attēlota
3.2. zīmējumā,
(situācijā, kas attēlota
3.2. zīmējumā,
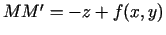 , jo punkta
, jo punkta 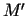 aplikāta ir
aplikāta ir
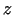 , bet punkta
, bet punkta 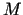 aplikāta ir
aplikāta ir  ).
).
Atsaucoties uz vienādību (3.3), var rakstīt, ka
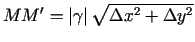 .
.
Tāpēc
Acīmredzami
![$ \frac{MN}{M_0{M}}\xrightarrow [\substack{x\rightarrow
x_0\\ y\rightarrow y_0}]{\/}0$](img433.gif) , jo
, jo
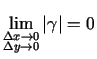 .
.
-
3.4. definīcija.
- Par funkcijas grafika
normāli punktā
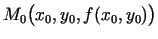 sauc
taisni, kas iet caur šo punktu un ir perpendikulāra šajā punktā
konkrētajai pieskarplaknei.
sauc
taisni, kas iet caur šo punktu un ir perpendikulāra šajā punktā
konkrētajai pieskarplaknei.
-
3.5. piemērs.
- Sastādīt pieskarplaknes un normāles vienādojumu
funkcijas
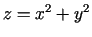 grafikam punktā, kura abscisa ir
grafikam punktā, kura abscisa ir 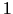 un
ordināta
un
ordināta 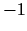 .
.
Atrod
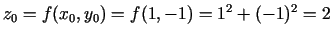 ,
, 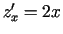 ;
;
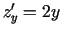 .
.
Izskaitļo
Pieskarplaknes vienādojums
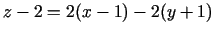
jeb
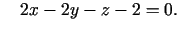
Tā kā normāle ir perpendikulāra pieskarplaknei,
tad šīs taisnes virziena vektors ir 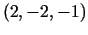 . Tādējādi
normāles vienādojums ir
. Tādējādi
normāles vienādojums ir



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.5. Saliktas funkcijas diferencēšana
Augstāk: 3. VAIRĀKU ARGUMENTU DIFERENCĒJAMAS FUNKCIJAS
Iepriekšējais: 3.3. Funkcijas diferenciāļa lietojumi tuvinātos aprēķinos
2002-06-21
![]() , kas ir nepārtraukta punktā
, kas ir nepārtraukta punktā
![]() .
.
![$ \frac{MN}{M_0M}
\xrightarrow[\substack{x\rightarrow x_0\\ y\rightarrow y_0}]{\/}0$](img417.gif) (skat. 3.2. zīm.).
(skat. 3.2. zīm.).
![]() Tā kā funkcija
Tā kā funkcija ![]() ir diferencējama punktā
ir diferencējama punktā
![]() , tad tā ir nepārtraukta šajā punktā un izpildās
sakarība
, tad tā ir nepārtraukta šajā punktā un izpildās
sakarība
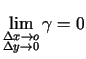 . Acīmredzami (3.1) ir plaknes, kas iet caur
punktu
. Acīmredzami (3.1) ir plaknes, kas iet caur
punktu
![$ \frac{MN}{M_0M}
\xrightarrow[\substack{x\rightarrow x_0\\ y\rightarrow y_0}]{\/}0$](img417.gif) (3.2. zīm.). No vienādības (3.2) atņem (3.1) un iegūst
(3.2. zīm.). No vienādības (3.2) atņem (3.1) un iegūst
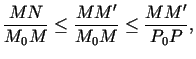
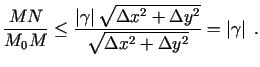
![$ \frac{MN}{M_0{M}}\xrightarrow [\substack{x\rightarrow
x_0\\ y\rightarrow y_0}]{\/}0$](img433.gif) , jo
, jo
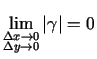 .
.