


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.4. Pieskarplakne
Augstāk: 3. VAIRĀKU ARGUMENTU DIFERENCĒJAMAS FUNKCIJAS
Iepriekšējais: 3.2. Punktā diferencējamas funkcijas pietiekamais nosacījums
Punktā  diferencējamai funkcijai
diferencējamai funkcijai  ir spēkā
vienādība
ir spēkā
vienādība
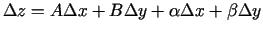 , kur
, kur 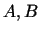 - skaitļi un
- skaitļi un
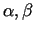 - bezgalīgi mazas
funkcijas, kad
- bezgalīgi mazas
funkcijas, kad
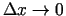 ,
,
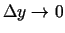 .
Tāpēc
.
Tāpēc
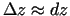 , kur
, kur
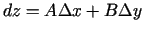 .
Pārveidojot šo aptuveno vienādību, iegūst, ka
.
Pārveidojot šo aptuveno vienādību, iegūst, ka
Šīs aptuvenās vienādības lietošanas
shēma ir šāda.
- Lielumu
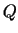 , kuram ir jāatrod tuvināta vērtība, uzraksta kā
funkcijas
, kuram ir jāatrod tuvināta vērtība, uzraksta kā
funkcijas  vērtību punktā
vērtību punktā
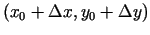 ,
t.i.,
,
t.i.,
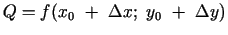 , kur punktu
, kur punktu  izvēlas tā, lai šajā punktā funkcijas vērtību varētu viegli
aprēķināt.
izvēlas tā, lai šajā punktā funkcijas vērtību varētu viegli
aprēķināt.
- Atrod
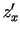 ,
, 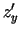 un izskaitļo funkcijas un tās parciālo
atvasinājumu vērtības punktā
un izskaitļo funkcijas un tās parciālo
atvasinājumu vērtības punktā  .
.
- No aptuvenās vienādības atrod
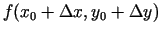 .
.
-
3.5. piezīme.
- Tuvinājums būs jo labāks, jo mazāki pēc moduļa būs
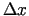 un
un 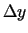 .
.
-
3.4. piemērs.
- Aprēķināt izteiksmes
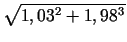 tuvinātu
vērtību.
tuvinātu
vērtību.
Šoreiz
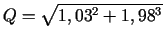 ,
,
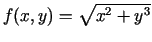 un
un
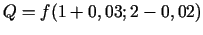 . Tādējādi
. Tādējādi 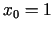 ,
, 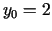 ,
,
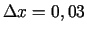 ,
,
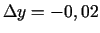 .
.
Atrod
Izskaitļo
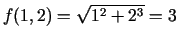 ;
;
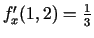 ,
,
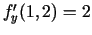 .
.
Pielieto aptuveno vienādību
un izskaitļo 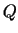 tuvinātu vērtību
tuvinātu vērtību
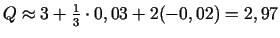 .
.
Tādējādi
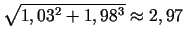 .
.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.4. Pieskarplakne
Augstāk: 3. VAIRĀKU ARGUMENTU DIFERENCĒJAMAS FUNKCIJAS
Iepriekšējais: 3.2. Punktā diferencējamas funkcijas pietiekamais nosacījums
2002-06-21
![]() diferencējamai funkcijai
diferencējamai funkcijai ![]() ir spēkā
vienādība
ir spēkā
vienādība
![]() , kur
, kur ![]() - skaitļi un
- skaitļi un
![]() - bezgalīgi mazas
funkcijas, kad
- bezgalīgi mazas
funkcijas, kad
![]() ,
,
![]() .
Tāpēc
.
Tāpēc
![]() , kur
, kur
![]() .
Pārveidojot šo aptuveno vienādību, iegūst, ka
.
Pārveidojot šo aptuveno vienādību, iegūst, ka
![]() . Tādējādi
. Tādējādi ![]() ,
, ![]() ,
,
![]() ,
,
![]() .
.
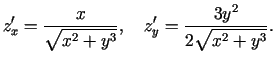
![]() .
.