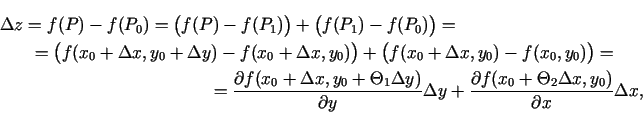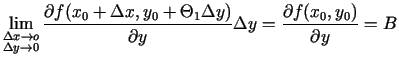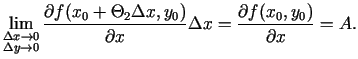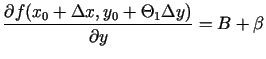Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.3. Funkcijas diferenciāļa lietojumi tuvinātos aprēķinos
Augstāk: 3. VAIRĀKU ARGUMENTU DIFERENCĒJAMAS FUNKCIJAS
Iepriekšējais: 3.1. Punktā diferencējama funkcija. Diferenciālis. Parciālie
Viena argumenta funkcijai punktā diferencējama funkcija ir tas
pats, kas funkcija, kurai eksistē šajā punktā atvasinājums.
Vairāku argumentu funkcijai parciālo atvasinājumu eksistence ir
šīs funkcijas diferencējamības tikai nepieciešamais nosacījums.
Piemēram, funkcijai
punktā  eksistē parciālie
atvasinājumi, pie tam
eksistē parciālie
atvasinājumi, pie tam
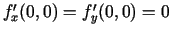 , jo
, jo
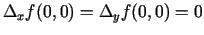 . Punktā
. Punktā  šī funkcija nav
nepārtraukta, tāpēc nav arī diferencējama.
šī funkcija nav
nepārtraukta, tāpēc nav arī diferencējama.
Lai funkcija būtu diferencējama punktā  , ar parciālo
atvasinājumu eksistenci vien nepietiek, bet vajag, lai šie
parciālie atvasinājumi būtu nepārtraukti šajā punktā.
, ar parciālo
atvasinājumu eksistenci vien nepietiek, bet vajag, lai šie
parciālie atvasinājumi būtu nepārtraukti šajā punktā.
-
3.3. teorēma.
- Punktā diferencējamas
funkcijas pietiekamais nosacījums.
Ja funkcijai  punkta
punkta
 apkārtnē eksistē
parciālie atvasinājumi
apkārtnē eksistē
parciālie atvasinājumi
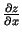 ,
,
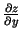 un tie ir nepārtraukti šajā
punktā, tad tā ir diferencējama punktā
un tie ir nepārtraukti šajā
punktā, tad tā ir diferencējama punktā
 .
.
 Izvēlas argumentu
Izvēlas argumentu 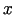 un
un 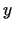 tādus pieaugumus
tādus pieaugumus
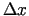 un
un 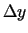 , lai punkts
, lai punkts
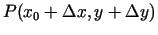 piederētu teorēmā minētajai apkārtnei (3.1. zīm.).
piederētu teorēmā minētajai apkārtnei (3.1. zīm.).
Pārveido funkcijas pieaugumu punktā  .
.
kur
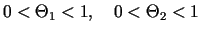 . (Starpībām, kas atradās
iekavās, tika pielietota Lagranža formula atbilstošajos
intervālos).
. (Starpībām, kas atradās
iekavās, tika pielietota Lagranža formula atbilstošajos
intervālos).
Tā kā parciālie atvasinājumi ir nepārtraukti punktā
 ,
tad
un
Tāpēc
un
kur
,
tad
un
Tāpēc
un
kur 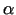 un
un
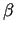 - bezgalīgi mazas funkcijas, kad
- bezgalīgi mazas funkcijas, kad
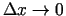 un
un
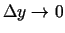 , bet
, bet 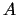 un
un 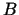 - skaitļi. Tātad
Tādējādi funkcija
- skaitļi. Tātad
Tādējādi funkcija  ir
diferencējama punktā
ir
diferencējama punktā
 .
.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.3. Funkcijas diferenciāļa lietojumi tuvinātos aprēķinos
Augstāk: 3. VAIRĀKU ARGUMENTU DIFERENCĒJAMAS FUNKCIJAS
Iepriekšējais: 3.1. Punktā diferencējama funkcija. Diferenciālis. Parciālie
2002-06-21
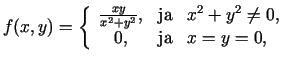
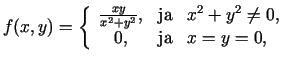
![]() punkta
punkta
![]() apkārtnē eksistē
parciālie atvasinājumi
apkārtnē eksistē
parciālie atvasinājumi
![]() ,
,
![]() un tie ir nepārtraukti šajā
punktā, tad tā ir diferencējama punktā
un tie ir nepārtraukti šajā
punktā, tad tā ir diferencējama punktā
![]() .
.
![]() Izvēlas argumentu
Izvēlas argumentu ![]() un
un ![]() tādus pieaugumus
tādus pieaugumus
![]() un
un ![]() , lai punkts
, lai punkts
![]() piederētu teorēmā minētajai apkārtnei (3.1. zīm.).
piederētu teorēmā minētajai apkārtnei (3.1. zīm.).