Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.2. Punktā diferencējamas funkcijas pietiekamais nosacījums
Augstāk: 3. VAIRĀKU ARGUMENTU DIFERENCĒJAMAS FUNKCIJAS
Iepriekšējais: 3. VAIRĀKU ARGUMENTU DIFERENCĒJAMAS FUNKCIJAS
-
3.1. definīcija.
- Funkciju
 sauc par diferencējamu
punktā
sauc par diferencējamu
punktā
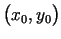 , ja tās pilno pieaugumu
, ja tās pilno pieaugumu 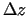 var izteikt
šādi:
kur
var izteikt
šādi:
kur 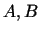 - skaitļi, bet
- skaitļi, bet
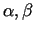 - bezgalīgi mazas funkcijas, kad
- bezgalīgi mazas funkcijas, kad
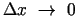 un
un
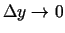 . Funkcijas pieauguma
. Funkcijas pieauguma 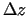 galveno
sastāvdaļu, t.i.,
galveno
sastāvdaļu, t.i.,
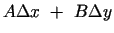 , sauc par šīs funkcijas
diferenciāli punktā
, sauc par šīs funkcijas
diferenciāli punktā  un apzīmē ar
un apzīmē ar 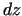 jeb
jeb
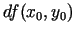 . Tādējādi
. Tādējādi
-
3.1. piezīme.
- Funkcijas pieauguma
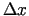 otru sastāvdaļu
otru sastāvdaļu
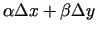 var pārveidot šādi:
kur
var pārveidot šādi:
kur
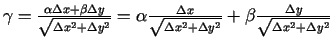 - bezgalīgi
maza funkcija, kad
- bezgalīgi
maza funkcija, kad
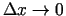 un
un
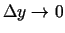 .
.
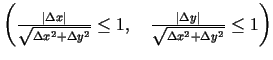 .
.
Tādējādi funkciju  sauc par diferencējamu punktā
sauc par diferencējamu punktā
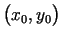 , ja tās pilno pieaugumu
, ja tās pilno pieaugumu 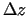 var izteikt
šādi:
var izteikt
šādi:
kur 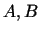 - skaitļi, bet
- skaitļi, bet 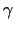 - bezgalīgi maza funkcija, kad
- bezgalīgi maza funkcija, kad
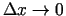 un
un
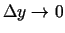 .
.
-
3.1. teorēma.
- (Punktā diferencējamas funkcijas nepieciešamais
nosacījums).
Ja funkcija  - diferencējama punktā
- diferencējama punktā  , tad eksistē robežas
, tad eksistē robežas
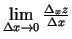 un
un
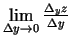 .
.
 No
No 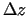 var iegūt
var iegūt
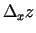 , ja
izvēlas
, ja
izvēlas
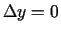 . Tādējādi
. Tādējādi
Seko, ka
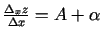 un eksistē
un eksistē
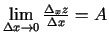 .
Analoģiski eksistē
.
Analoģiski eksistē
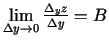 .
.
-
3.2. definīcija.
- Ja funkcija
 ir definēta
punktā
ir definēta
punktā  un tā apkārtnē, eksistē
un tā apkārtnē, eksistē
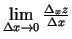 , tad šo robežu sauc par šīs funkcijas
parciālo atvasinājumu pēc
, tad šo robežu sauc par šīs funkcijas
parciālo atvasinājumu pēc 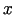 punktā
punktā  un
apzīmē
un
apzīmē
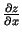 ,
, 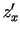 ,
,
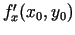 .
Tādējādi
.
Tādējādi
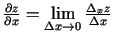 . Analoģiski definē
. Analoģiski definē
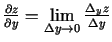 .
.
-
3.2. piezīme.
-

- 3.1. teorēmu var formulēt šādi.
Ja funkcija  - diferencējama punktā
- diferencējama punktā  , tad šajā
punktā tai eksistē parciālie atvasinājumi
, tad šajā
punktā tai eksistē parciālie atvasinājumi
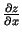 un
un
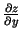 .
.
- Funkcijas
 diferenciāli
diferenciāli 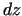 var izteikt šādi:
var izteikt šādi:
- Parasti argumentu pieaugumus
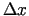 un
un 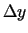 apzīmē
atbilstoši
apzīmē
atbilstoši 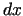 un
un 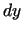 , tāpēc
, tāpēc
- 3.1. teorēmai apgrieztais apgalvojums nav spēkā.
-
3.2. teorēma.
- (Punktā diferencējamas funkcijas nepieciešamais
nosacījums).
Ja funkcija  - diferencējama punktā
- diferencējama punktā  , tad šajā punktā tā ir
nepārtraukta.
, tad šajā punktā tā ir
nepārtraukta.
(Pierādīt patstāvīgi).
-
3.3. piezīme.
-

- Arī šoreiz apgrieztā teorēma nav spēkā. Piemēram, funkcija
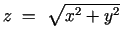 ir nepārtraukta punktā
ir nepārtraukta punktā  , tomēr šajā punktā
tai neeksistē parciālie atvasinājumi un, proti, tā nav
diferencējama punktā
, tomēr šajā punktā
tai neeksistē parciālie atvasinājumi un, proti, tā nav
diferencējama punktā  . (Pamatot patstāvīgi!).
. (Pamatot patstāvīgi!).
- Tā kā parciālo atvasinājumu definīcijas ir analoģiskas viena
argumenta funkcijas atvasinājuma definīcijai, tad parciālos
atvasinājumus atrod pēc tām pašām formulām un tiem pašiem likumiem,
kādi tika apskatīti viena argumenta funkcijām. Svarīgi atzīmēt, ka
atrodot
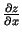 ,
, 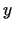 uzskata ne par
mainīgo, bet par konstanti. Analoģiski, kad atrod
uzskata ne par
mainīgo, bet par konstanti. Analoģiski, kad atrod
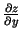 ,
, 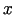 uzskata par konstanti.
uzskata par konstanti.
-
3.1. piemērs.
- Atrast funkcijas
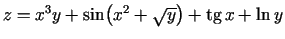 parciālos atvasinājumus.
parciālos atvasinājumus.
Vispirms 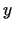 uzskata par konstanti un atrod
Analoģiski
uzskata par konstanti un atrod
Analoģiski
-
3.2. piemērs.
- Atrast funkcijas
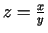 diferenciāli
diferenciāli 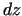 punktā
punktā 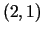 , ja
, ja
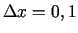 ;
;
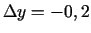 .
.
Atrod
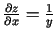 un
un
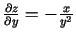 . Izskaitļo parciālo atvasinājumu vērtības punktā
. Izskaitļo parciālo atvasinājumu vērtības punktā
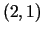 .
.
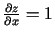 ;
;
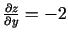 . Funkcijas diferenciālis
Tādējādi
. Funkcijas diferenciālis
Tādējādi
Apskata funkciju  , kurai punktā
, kurai punktā  eksistē
parciālie atvasinājumi pie fiksētas vērtības
eksistē
parciālie atvasinājumi pie fiksētas vērtības 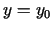 . Ģeometriski
tas nozīmē, ka virsma
. Ģeometriski
tas nozīmē, ka virsma  tiek šķelta ar plakni
tiek šķelta ar plakni 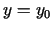 (šī
plakne paralēla koordinātu plaknei
(šī
plakne paralēla koordinātu plaknei 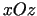 ). Šķēlumā iegūst līniju,
kas iet caur doto punktu. Virziena koeficients pieskarei, kas
konstruēta šai līnijai punktā
). Šķēlumā iegūst līniju,
kas iet caur doto punktu. Virziena koeficients pieskarei, kas
konstruēta šai līnijai punktā  , būs vienāds ar
, būs vienāds ar
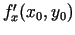 . Analoģiski
. Analoģiski
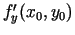 ir virziena
koeficients pieskarei, kas konstruēta punktā
ir virziena
koeficients pieskarei, kas konstruēta punktā  līnija, pa kuru virsma
līnija, pa kuru virsma  šķeļas ar plakni
šķeļas ar plakni 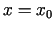 .
.
-
3.4. piezīme.
- Analoģiski rīkojoties, var definēt punktā
diferencējamu triju, četru utt. argumentu funkciju, tās parciālos
atvasinājumus un diferenciāli. Atrodot šādas funkcijas parciālo
atvasinājumu pēc kāda mainīgā, pārējos argumentus uzskata par
konstantēm.
-
3.3. piemērs.
- Atrast funkcijas
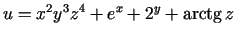 parciālos atvasinājumus.
parciālos atvasinājumus.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.2. Punktā diferencējamas funkcijas pietiekamais nosacījums
Augstāk: 3. VAIRĀKU ARGUMENTU DIFERENCĒJAMAS FUNKCIJAS
Iepriekšējais: 3. VAIRĀKU ARGUMENTU DIFERENCĒJAMAS FUNKCIJAS
2002-06-21
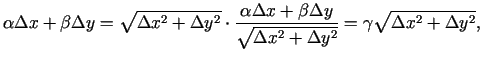
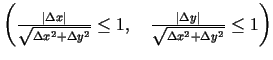 .
.
![]() sauc par diferencējamu punktā
sauc par diferencējamu punktā
![]() , ja tās pilno pieaugumu
, ja tās pilno pieaugumu ![]() var izteikt
šādi:
var izteikt
šādi:
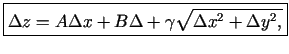
![]() - diferencējama punktā
- diferencējama punktā ![]() , tad eksistē robežas
, tad eksistē robežas
![]() un
un
![]() .
.
![]() No
No ![]() var iegūt
var iegūt
![]() , ja
izvēlas
, ja
izvēlas
![]() . Tādējādi
. Tādējādi
![]() - diferencējama punktā
- diferencējama punktā ![]() , tad šajā punktā tā ir
nepārtraukta.
, tad šajā punktā tā ir
nepārtraukta.
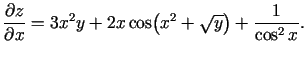
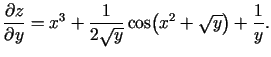
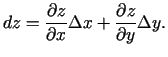
![]() , kurai punktā
, kurai punktā ![]() eksistē
parciālie atvasinājumi pie fiksētas vērtības
eksistē
parciālie atvasinājumi pie fiksētas vērtības ![]() . Ģeometriski
tas nozīmē, ka virsma
. Ģeometriski
tas nozīmē, ka virsma ![]() tiek šķelta ar plakni
tiek šķelta ar plakni ![]() (šī
plakne paralēla koordinātu plaknei
(šī
plakne paralēla koordinātu plaknei ![]() ). Šķēlumā iegūst līniju,
kas iet caur doto punktu. Virziena koeficients pieskarei, kas
konstruēta šai līnijai punktā
). Šķēlumā iegūst līniju,
kas iet caur doto punktu. Virziena koeficients pieskarei, kas
konstruēta šai līnijai punktā ![]() , būs vienāds ar
, būs vienāds ar
![]() . Analoģiski
. Analoģiski
![]() ir virziena
koeficients pieskarei, kas konstruēta punktā
ir virziena
koeficients pieskarei, kas konstruēta punktā ![]() līnija, pa kuru virsma
līnija, pa kuru virsma ![]() šķeļas ar plakni
šķeļas ar plakni ![]() .
.