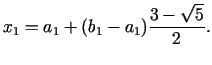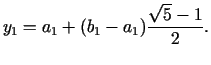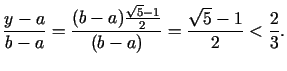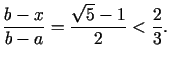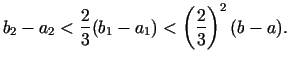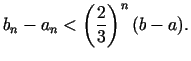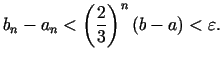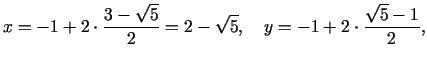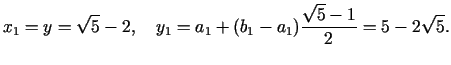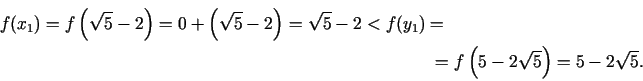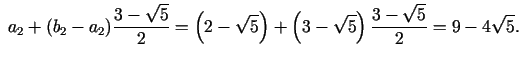Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.3. Minimuma punkta meklēšanas metodes vairāku
Augstāk: 2.2. Minimuma punkta meklēšanas metodes
Iepriekšējais: 2.2.2. Fibonači skaitļu metode
Iepriekšējā apakšparagrāfā unimodālas funkcijas ekstrēma
meklēšanas procesā nogrieznis ![$ [a;b]$](img460.gif) tika sadalīts trīs daļās
tika sadalīts trīs daļās
![$ [a;x]$](img568.gif) ,
, ![$ [x;y]$](img569.gif) un
un ![$ [y;b]$](img570.gif) , kur punkti
, kur punkti  un
un 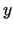 tika definēti
ar Fibonači skaitļu palīdzību. Lietojot zelta šķēluma metodi,
izmanto tā saucamos zelta šķēluma punktus. Aplūkosim zīmējumā
attēloto nogriezni
tika definēti
ar Fibonači skaitļu palīdzību. Lietojot zelta šķēluma metodi,
izmanto tā saucamos zelta šķēluma punktus. Aplūkosim zīmējumā
attēloto nogriezni ![$ [a;b]$](img460.gif) ar dalījuma punktiem
ar dalījuma punktiem  un
un 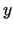 .
Nogriežņa
.
Nogriežņa ![$ [a;b]$](img460.gif) punktu
punktu  sauc par zelta šķēluma
punktu, ja mazākā nogriežņa
sauc par zelta šķēluma
punktu, ja mazākā nogriežņa ![$ [a;x]$](img568.gif) attiecība pret lielāko
nogriezni
attiecība pret lielāko
nogriezni ![$ [x;b]$](img571.gif) ir vienāda ar lielākā nogriežņa attiecību pret
visu nogriezni
ir vienāda ar lielākā nogriežņa attiecību pret
visu nogriezni ![$ [a;b]$](img460.gif) (skat. 2.1. zīm.), t.i.,
Analoģiski punkts
(skat. 2.1. zīm.), t.i.,
Analoģiski punkts 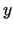 tiek definēts tā, lai
Viegli redzēt, ka
tiek definēts tā, lai
Viegli redzēt, ka
Var pārbaudīt, ka punkti  un
un 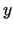 ir novietoti nogrieznī
ir novietoti nogrieznī ![$ [a,b]$](img496.gif) simetriski, t.i.,
simetriski, t.i.,
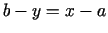 .
.
2.1. zīm. Nogriežņa ![$ [a;b]$](img460.gif) zelta šķēluma punkti
zelta šķēluma punkti  un
un 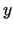 .
.
Zelta šķēluma metodes būtību izsaka nākamā
teorēma.
-
2.1. teorēma.
- Nogriežņa
![$ [a;b]$](img460.gif) zelta šķēluma punkts
zelta šķēluma punkts  ir
zelta šķēluma punkts lielākajam no nogriežņiem, kuros nogriezni
ir
zelta šķēluma punkts lielākajam no nogriežņiem, kuros nogriezni
![$ [a;b]$](img460.gif) sadala otrs zelta šķēluma punkts, t.i.,
sadala otrs zelta šķēluma punkts, t.i.,  ir zelta
šķēluma punkts nogrieznim
ir zelta
šķēluma punkts nogrieznim ![$ [a;y]$](img579.gif) . Analoģiski
. Analoģiski 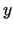 ir zelta
šķēlums nogrieznim
ir zelta
šķēlums nogrieznim ![$ [x;b]$](img571.gif) .
.
 Jāpierāda, ka
Jāpierāda, ka
Tiešām,
Analoģiski var pierādīt, ka 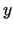 ir nogriežņa
ir nogriežņa ![$ [x,b]$](img587.gif) zelta šķēluma
punkts.
zelta šķēluma
punkts.
Minimuma punkta meklēšana saskaņā ar
zelta šķēluma metodi notiek šādi.
Salīdzina
funkcijas 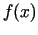 vērtības zelta šķēluma punktos
vērtības zelta šķēluma punktos  un
un 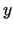 . Ir
iespējami divi gadījumi:
. Ir
iespējami divi gadījumi:
a) ja
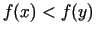 , tad
, tad
![$ [a;y]$](img579.gif) ir minimuma punkta lokalizācijas intervāls;
ir minimuma punkta lokalizācijas intervāls;
b) ja
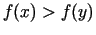 , tad
, tad ![$ [x;b]$](img571.gif) ir minimuma punkta
lokalizācijas intervāls.
ir minimuma punkta
lokalizācijas intervāls.
a) gadījumā jaunais
intervāls ir
![$ [a_{1};b_{1}]=[a;y]$](img590.gif) un lielākais zelta šķēluma
punkts
un lielākais zelta šķēluma
punkts 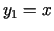 ir zināms, bet otro, mazāko, var aprēķināt pēc
formulas
ir zināms, bet otro, mazāko, var aprēķināt pēc
formulas
Tālāk salīdzina 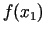 un
un 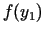 un atkārto
procedūru.
un atkārto
procedūru.
b) gadījumā jaunais intervāls ir
![$ [a_{1};b_{1}]=[x;b]$](img593.gif) un
un 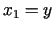 ir jaunā intervāla mazākais
zelta šķēluma punkts. Otrais, lielākais, zelta šķēluma punkts ir
ir jaunā intervāla mazākais
zelta šķēluma punkts. Otrais, lielākais, zelta šķēluma punkts ir
Tālāk salīdzina 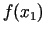 un
un 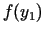 un atrod jauno
lokalizācijas intervālu.
un atrod jauno
lokalizācijas intervālu.
Aprēķinu
precizitāte. Cik iterāciju jāņem, lai ekstrēma punkts būtu
aprēķināts ar doto precizitāti, t.i., lai lielums
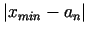 (vai lielums
(vai lielums
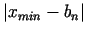 ) būtu mazāks par
doto precizitāti
) būtu mazāks par
doto precizitāti
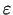 ?
?
Lai sniegtu
atbildi uz šo jautājumu, ievērosim, ka
Analoģiski iegūsim
Tas nozīmē, ka, gan a) gadījumā, gan b) gadījumā, jaunā
lokalizācijas intervāla
![$ [a_{1};b_{1}]$](img471.gif) garums ir mazāks par
garums ir mazāks par
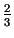 no iepriekšējā intervāla garuma. Nākamajā solī
intervāla
no iepriekšējā intervāla garuma. Nākamajā solī
intervāla
![$ [a_{2};b_{2}]$](img499.gif) garums apmierina nevienādību
Acīmredzot, ir spēkā novērtējums
garums apmierina nevienādību
Acīmredzot, ir spēkā novērtējums
Tas nozīmē, ka, lai aprēķinātu 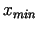 ar precizitāti
ar precizitāti
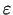 , pietiek ar tādu
, pietiek ar tādu 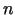 , lai izpildītos nevienādība
Tas ir iespējams: par
, lai izpildītos nevienādība
Tas ir iespējams: par 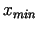 tuvinājumu var ņemt gan
tuvinājumu var ņemt gan 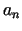 ,
gan
,
gan 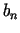 , gan intervāla viduspunktu
, gan intervāla viduspunktu
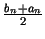 .
.
-
2.4. piemērs.
- Atradīsim funkcijas f(x) =
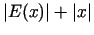 minimumu
intervālā
minimumu
intervālā
![$ [a;b] = [-1;1]$](img607.gif) .
.
Pirmajā solī
Jaunais intervāls
Nākamajā solī
Salīdzinot funkcijas vērtības, iegūstam
Jaunais intervāls
Jaunie dalījuma punkti
Salīdzinot
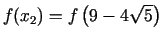 un
un
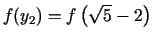 , iegūstam jaunu lokalizācijas intervālu
utt., kamēr minimuma punkts nebūs atrasts ar vajadzīgo
precizitāti.
, iegūstam jaunu lokalizācijas intervālu
utt., kamēr minimuma punkts nebūs atrasts ar vajadzīgo
precizitāti.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.3. Minimuma punkta meklēšanas metodes vairāku
Augstāk: 2.2. Minimuma punkta meklēšanas metodes
Iepriekšējais: 2.2.2. Fibonači skaitļu metode
2002-05-04
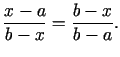
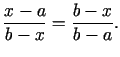
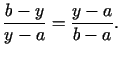
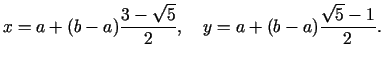
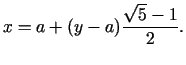
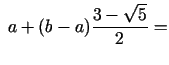
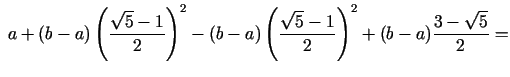
![$\displaystyle \;a + \Biggl[ {a + (b - a){\frac{\sqrt 5 - 1}{2}} - a} \Biggr]{\frac{\sqrt 5 - 1}{2}}+$](img584.gif)
![$\displaystyle \qquad\qquad\qquad\qquad\qquad\qquad\; + (b - a)\Biggl[ {\frac{3 - \sqrt 5 }{2} - \left( {\frac{\sqrt 5 - 1}{2}} \right)^2} \Biggr]=$](img585.gif)
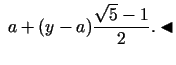
![]() ir nogriežņa
ir nogriežņa ![]() zelta šķēluma
punkts.
zelta šķēluma
punkts.