


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.2.3. Zelta šķēluma metode
Augstāk: 2.2. Minimuma punkta meklēšanas metodes
Iepriekšējais: 2.2.1. Dihotomijas metode (jeb intervāla dalīšanas
Dotā metode balstās uz Fibonači skaitļu izmantošanu. Fibonači
skaitļi ir veseli skaitļi, kurus iegūst pēc rekurentas formulas:
Pirmie Fibonači skaitļi ir uzrādīti tabulā.
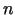 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
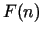 |
1 |
1 |
2 |
3 |
5 |
8 |
13 |
21 |
34 |
55 |
89 |
144 |
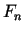 var aprēķināt pēc formulas
var aprēķināt pēc formulas
Pieņemsim, ka 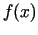 ir unimodāla funkcija intervālā
ir unimodāla funkcija intervālā ![$ [a;b]$](img460.gif) .
Minimuma punkta meklēšanas shēma saskaņā ar Fibonači metodi ir
šāda.
.
Minimuma punkta meklēšanas shēma saskaņā ar Fibonači metodi ir
šāda.
Dalām intervālu ![$ [a;b]$](img460.gif) trīs daļās ar punktiem
(uzskatām, ka
trīs daļās ar punktiem
(uzskatām, ka 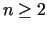 ). Punkti
). Punkti  un
un 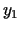 ir novietoti
simetriski intervālā
ir novietoti
simetriski intervālā ![$ [a,b]$](img496.gif) , jo
, jo
un
Tālāk izvēlēsimies jaunu intervālu
![$ [a_{2};b_{2}]$](img499.gif) atkarībā no tā,
kura vērtība,
atkarībā no tā,
kura vērtība, 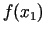 vai
vai 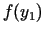 , ir lielāka:
, ir lielāka:
a) ja
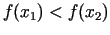 , tad jaunais intervāls ir
, tad jaunais intervāls ir
![$ [a_{2};b_{2}] = [a;y_{1}]$](img502.gif) ;
;
b) ja
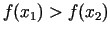 , tad jaunais intervāls ir
, tad jaunais intervāls ir
![$ [a_{2};b_{2}] = [x_{1};b]$](img503.gif) .
.
Abos gadījumos iegūto intervālu garumi ir vienādi, jo
Jaunā intervāla
![$ [a_{2};b_{2}]$](img499.gif) garums ir
garums ir
Aplūkosim a) gadījumu, kad
![$ [a_{2};b_{2}] = [a;y_{1}]$](img502.gif) . Jaunie
dalījuma punkti ir
. Jaunie
dalījuma punkti ir
Atzīmēsim, ka
tātad jaunajā intervālā lielākais sadalījuma punkts sakrīt ar
iepriekšējā intervāla mazāko sadalījuma punktu. Tālāk salīdzinām
vērtības 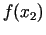 un
un 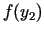 un, atkarībā no salīdzināšanas
rezultātiem, par jauno minimuma punkta lokalizācijas intervālu
un, atkarībā no salīdzināšanas
rezultātiem, par jauno minimuma punkta lokalizācijas intervālu
![$ [a_{2};b_{2}]$](img499.gif) izvēlamies vai nu intervālu
izvēlamies vai nu intervālu
![$ [a_{2};y_{2}]$](img510.gif) (ja
(ja
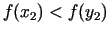 ), vai arī intervālu
), vai arī intervālu
![$ [x_{2};b_{2}]$](img512.gif) (ja
(ja
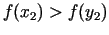 ). Iesakām lasītājam patstāvīgi pārliecināties,
ka jaunā intervāla garums ir
). Iesakām lasītājam patstāvīgi pārliecināties,
ka jaunā intervāla garums ir
Aplūkosim b) gadījumu, kad
![$ [a_{2};b_{2}] = [x_{1};b]$](img503.gif) . Jaunie
dalījuma punkti ir
. Jaunie
dalījuma punkti ir
bet tagad
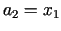 atšķirībā no a) gadījuma. Atzīmēsim, ka
atšķirībā no a) gadījuma. Atzīmēsim, ka
t.i., jaunajā intervālā mazākais dalījuma punkts sakrīt ar
iepriekšējā intervāla lielāko dalījuma punktu. Salīdzinām vērtības
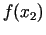 un
un 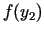 un, atkarībā no salīdzināšanas rezultāta,
par jauno minimuma punkta lokalizācijas intervālu
un, atkarībā no salīdzināšanas rezultāta,
par jauno minimuma punkta lokalizācijas intervālu
![$ [a_{2};b_{2}]$](img499.gif) izvēlamies vai nu intervālu
izvēlamies vai nu intervālu
![$ [a_{2};y_{2}]$](img510.gif) (ja
(ja
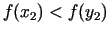 ), vai arī intervālu
), vai arī intervālu
![$ [x_{2};b_{2}]$](img512.gif) (ja
(ja
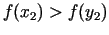 ). Jaunā intervāla
). Jaunā intervāla
![$ [a_{3};b_{3}]$](img484.gif) garums ir
garums ir
Rezumēsim iegūtos rezultātus. Solī ar numuru 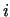 iegūstam jaunu
lokalizācijas intervālu
iegūstam jaunu
lokalizācijas intervālu
![$ [a_{i};b_{i}]$](img520.gif) (uzskatām ka
(uzskatām ka
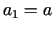 ,
, 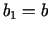 ), kura garums ir
), kura garums ir
Dalījuma punkti:
Pēc 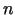 soļiem
un
soļiem
un
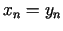 . Intervāla
. Intervāla
![$ [a_{n};b_{n}]$](img527.gif) garums ir
garums ir
Aprēķinu algoritms ir skaidrs, paliek viens neatrisināts
jautājums: kādu 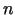 izvēlēties?
izvēlēties?
Jo lielāks ir
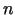 , jo precīzāk varam atrast minimuma punktu, bet līdz ar to būs
jāveic vairāk aprēķinu. Tātad, ja ir uzdots skaitlis
, jo precīzāk varam atrast minimuma punktu, bet līdz ar to būs
jāveic vairāk aprēķinu. Tātad, ja ir uzdots skaitlis
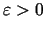 (- precizitāte) un ir jāaprēķina minimuma punkta
(- precizitāte) un ir jāaprēķina minimuma punkta
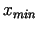 tuvinājumu
tuvinājumu 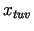 tā, lai izpildītos nevienādība
tā, lai izpildītos nevienādība
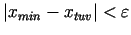 , tad
, tad 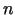 ir jāizvēlās tā, lai
ir jāizvēlās tā, lai
Šajā gadījumā intervāla
![$ [a_{n};b_{n}]$](img527.gif) garums nepārsniegs
garums nepārsniegs
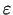 , un par minimuma punkta tuvinājumu var ņemt jebkuru
šī intervāla punktu, piemēram, tā viduspunktu
, un par minimuma punkta tuvinājumu var ņemt jebkuru
šī intervāla punktu, piemēram, tā viduspunktu
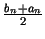 .
.
-
2.3. piemērs.
- Aprēķināt funkcijas
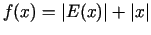 minimuma punktu intervālā
minimuma punktu intervālā ![$ [-1, 1]$](img532.gif) ar precizitāti
ar precizitāti
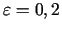 .
.
1. solis. Skaitļa 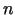 izvēle.
izvēle.
Izvēlēsimies tādu 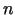 , lai
, lai
Ja 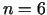 , tad
2. solis. Dalījuma punkti:
, tad
2. solis. Dalījuma punkti:
pie tam
Jaunais intervāls
3. solis. Dalījuma punkti
pie tam
Jaunais intervāls
4. solis. Dalījuma punkti
pie tam
Jaunais intervāls
5. solis. Dalījuma punkti
pie tam
Jaunais intervāls
6. solis. Dalījuma punkti
pie tam
Jaunais intervāls
7. solis. Pēdējā intervāla garums
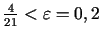 . Prasītā precizitāte ir sasniegta. Procesu var
beigt. Par funkcijas minimuma punktu var ņemt intervāla
viduspunktu
. Prasītā precizitāte ir sasniegta. Procesu var
beigt. Par funkcijas minimuma punktu var ņemt intervāla
viduspunktu
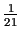 . Viegli redzēt, ka reālais minimuma
punkts ir nulle, un tuvinājums atšķiras no tā par vērtību, kas ir
mazāka par
. Viegli redzēt, ka reālais minimuma
punkts ir nulle, un tuvinājums atšķiras no tā par vērtību, kas ir
mazāka par
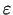 .
.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.2.3. Zelta šķēluma metode
Augstāk: 2.2. Minimuma punkta meklēšanas metodes
Iepriekšējais: 2.2.1. Dihotomijas metode (jeb intervāla dalīšanas
2002-05-04
![$\displaystyle F_n=\frac{1}{\sqrt 5 }\left[ {\left( {\frac{1 + \sqrt 5 }{2}}
\right)^n - \left( {\frac{1 - \sqrt 5 }{2}} \right)^n}
\right]\;\;(n = 1,2,\ldots).
$](img492.gif)
![]() ir unimodāla funkcija intervālā
ir unimodāla funkcija intervālā ![]() .
Minimuma punkta meklēšanas shēma saskaņā ar Fibonači metodi ir
šāda.
.
Minimuma punkta meklēšanas shēma saskaņā ar Fibonači metodi ir
šāda.
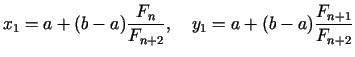
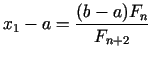
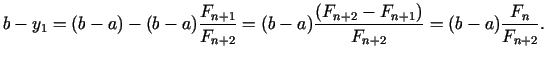
![]() atkarībā no tā,
kura vērtība,
atkarībā no tā,
kura vērtība, ![]() vai
vai ![]() , ir lielāka:
, ir lielāka:
![]() , tad jaunais intervāls ir
, tad jaunais intervāls ir
![]() ;
;
![]() , tad jaunais intervāls ir
, tad jaunais intervāls ir
![]() .
.
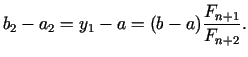
![]() . Jaunie
dalījuma punkti ir
. Jaunie
dalījuma punkti ir
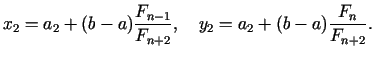
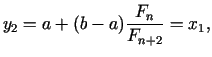
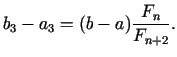
![]() . Jaunie
dalījuma punkti ir
. Jaunie
dalījuma punkti ir
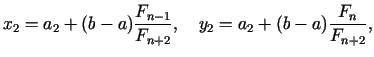
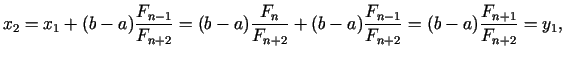
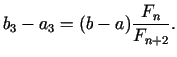
![]() iegūstam jaunu
lokalizācijas intervālu
iegūstam jaunu
lokalizācijas intervālu
![]() (uzskatām ka
(uzskatām ka
![]() ,
, ![]() ), kura garums ir
), kura garums ir
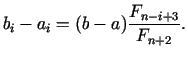
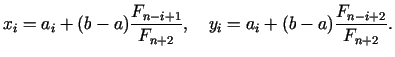
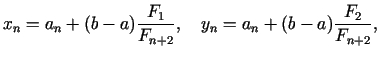
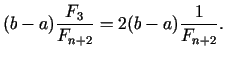
![]() izvēlēties?
izvēlēties?
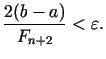
![]() izvēle.
izvēle.
![]() , lai
, lai
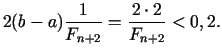
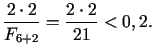
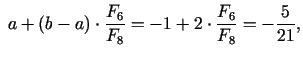
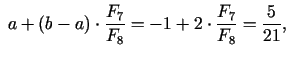
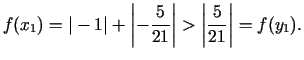
![$\displaystyle [a_{2};b_{2}]=[x_{1};b]=\left[-\frac{5}{21};1\right],\;\; x_{2}=y_{1}=\frac{5}{21}.$](img541.gif)
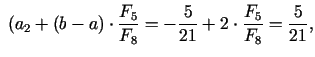
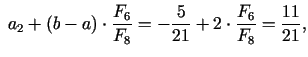
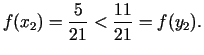
![$\displaystyle [a_{3};b_{3}]=[a_{2};y_{2}]=\left[-\frac{5}{21};\frac{11}{21}\right],\;\; y_{3}=x_{2}=\frac{5}{21}.$](img547.gif)
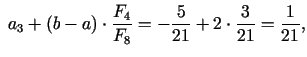
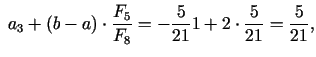
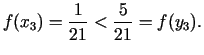
![$\displaystyle [a_{4};b_{4}] = [a_{3};y_{3}] = \left[-\frac{5}{21};\frac{5}{21}\right],\;\; y_{4} = x_{3} = \frac{1 }{21}.$](img553.gif)
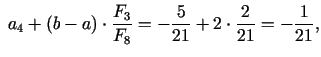
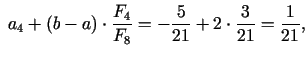
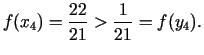
![$\displaystyle [a_{5};b_{5}]=[x_{4};b_{4}]=\left[-\frac{1}{21};\frac{5}{21}\right],\;\; x_{5} = y_{4} = \frac{1}{21}.$](img559.gif)
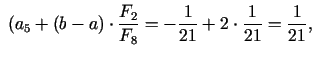
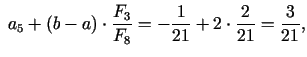
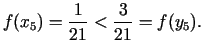
![$\displaystyle [a_{6};b_{6}]=[a_{5};y_{5}]=\left[-\frac{1}{21};\frac{3}{21}\right].$](img565.gif)