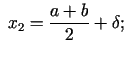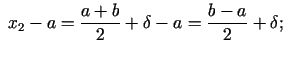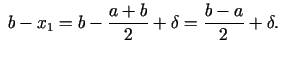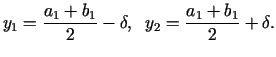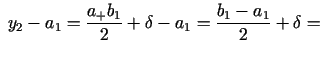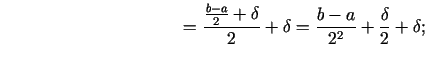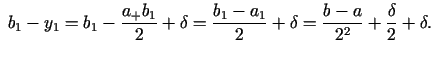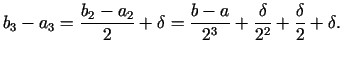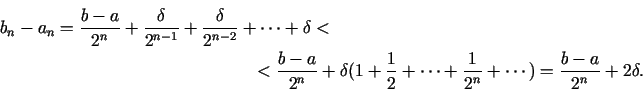Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.2.2. Fibonači skaitļu metode
Augstāk: 2.2. Minimuma punkta meklēšanas metodes
Iepriekšējais: 2.2. Minimuma punkta meklēšanas metodes
Uzdevums. Atrast unimodālas funkcijas minimuma punktu ar
precizitāti
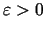 .
.
Te
nepieciešams paskaidrojums. Atrast funkcijas minimuma punktu
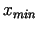 (kura vērtība nav zināma) ar precizitāti
(kura vērtība nav zināma) ar precizitāti
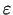 nozīme atrast tādu punkta
nozīme atrast tādu punkta 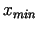 tuvināto vērtību
tuvināto vērtību 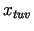 ,
kura apmierina nosacījumu
,
kura apmierina nosacījumu
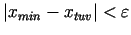 .
.
Uzdevuma risinājums. Pieņemsim, ka unimodāla funkcija  ir definēta segmentā
ir definēta segmentā ![$ [a;b]$](img460.gif) . Sadalīsim segmentu
. Sadalīsim segmentu ![$ [a;b]$](img460.gif) trīs
daļās
trīs
daļās
kur punkti  un
un 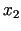 apmierina nosacījumus
apmierina nosacījumus
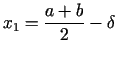
un
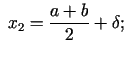
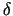 - pietiekami mazs skaitlis (
- pietiekami mazs skaitlis (
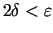 ).
Atzīmēsim, ka punkts
).
Atzīmēsim, ka punkts
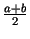 ir intervāla
ir intervāla ![$ [a;b]$](img460.gif) viduspunkts, un punkti
viduspunkts, un punkti  un
un 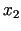 atrodas gandrīz
intervāla vidū (ja
atrodas gandrīz
intervāla vidū (ja 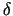 ir mazs), taču dažādās pusēs no
viduspunkta.
ir mazs), taču dažādās pusēs no
viduspunkta.
Salīdzināsim funkcijas 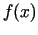 vērtības punktos
vērtības punktos  un
un 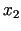 . Gadījumā, ja
. Gadījumā, ja
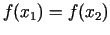 , meklētais minimuma punkts noteikti atrodas intervālā
, meklētais minimuma punkts noteikti atrodas intervālā
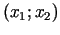 (jo pretējā gadījumā funkcija
(jo pretējā gadījumā funkcija  nebūtu
unimodāla). Tā kā intervāla garums ir
nebūtu
unimodāla). Tā kā intervāla garums ir
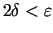 , tad
par minimuma punkta tuvinājumu var izvēlēties intervāla
viduspunktu. Gadījumā, ja
, tad
par minimuma punkta tuvinājumu var izvēlēties intervāla
viduspunktu. Gadījumā, ja
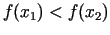 , no
Apgalvojuma izriet, ka minimuma punkts
, no
Apgalvojuma izriet, ka minimuma punkts 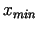 (tas ir
viens vienīgs, jo
(tas ir
viens vienīgs, jo  ir unimodāla) atrodas intervālā
ir unimodāla) atrodas intervālā 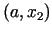 .
Ja
.
Ja
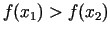 , tad
, tad
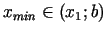 . Abos gadījumos
jaunā intervāla, kuru apzīmēsim ar
. Abos gadījumos
jaunā intervāla, kuru apzīmēsim ar
![$ [a_{1};b_{1}]$](img471.gif) , garums ir
viens un tas pats:
, garums ir
viens un tas pats:
Atkārtojot analoģisku procedūru jaunajā intervālā
![$ [a_{1};b_{1}]$](img471.gif) ,
iegūstam jaunus dalījuma punktus:
,
iegūstam jaunus dalījuma punktus:
Ja
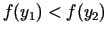 , tad jaunais intervāls
, tad jaunais intervāls
![$ [a_{2};b_{2}]=
[a_{1},y_{2}]$](img477.gif) , bet, ja
, bet, ja
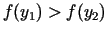 , tad jaunais intervāls
, tad jaunais intervāls
![$ [a_{2};b_{2}]=[y_{1};b_{1}]$](img479.gif) . Abos gadījumos jauniegūtā intervāla
garums ir viens un tas pats:
. Abos gadījumos jauniegūtā intervāla
garums ir viens un tas pats:
Nākamajā (trešajā) solī iegūstam intervālu
![$ [a_{3};b_{3}]$](img484.gif) ar
garumu
Pēc indukcijas,
ar
garumu
Pēc indukcijas, 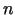 -tajā solī
-tajā solī
Pēdējās izteiksmes iegūšanai tika lietota bezgalīgi dilstošas
ģeometriskās progresijas locekļu summas formula. Aprēķini ir
jābeidz, ja
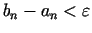 , iegūstot minimuma punkta
tuvinājumu ar vajadzīgo precizitāti.
, iegūstot minimuma punkta
tuvinājumu ar vajadzīgo precizitāti.
Viens no
svarīgākajiem metodes efektivitātes parametriem - aprēķinu apjoms.
Metode skaitās efektīva, ja ir jāaprēķina pēc iespējas
mazāk funkciju vērtību utt. Lietojot dihotomijas metodi, funkcijas
 vērtības ir jāaprēķina
vērtības ir jāaprēķina 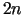 reizes.
reizes.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.2.2. Fibonači skaitļu metode
Augstāk: 2.2. Minimuma punkta meklēšanas metodes
Iepriekšējais: 2.2. Minimuma punkta meklēšanas metodes
2002-05-04
![]() .
.
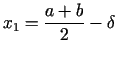 un
un