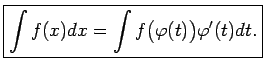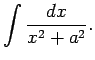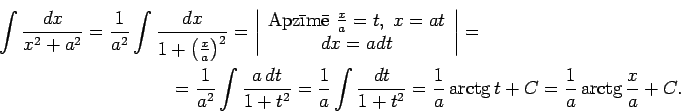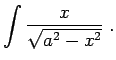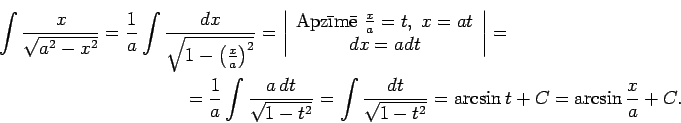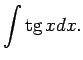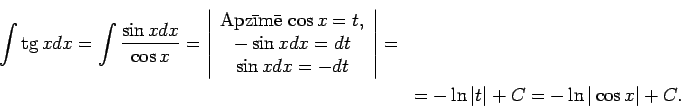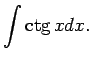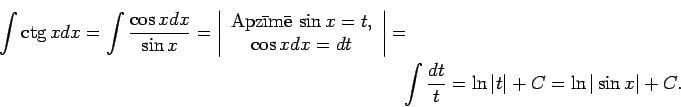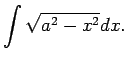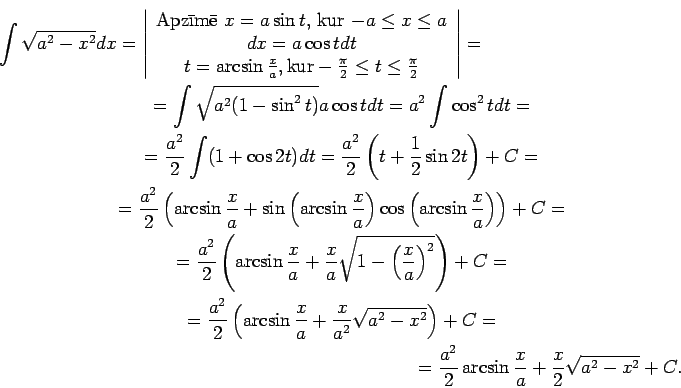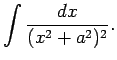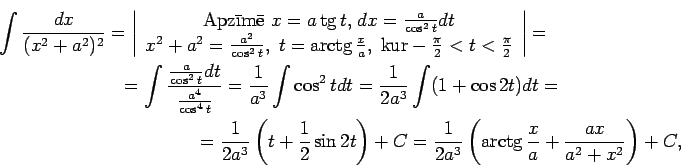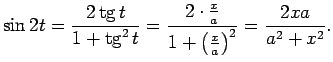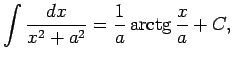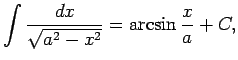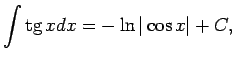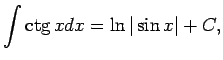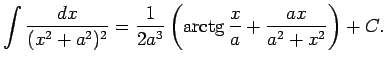Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.5. Racionālu funkciju integrēšana
Augstāk: 1.4. Integrēšanas pamatmetodes
Iepriekšējais: 1.4.1. Parciālā integrēšana
-
1.1. teorēma.
- Ja
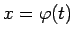 ir stingri monotona un
diferencējama
intervālā
ir stingri monotona un
diferencējama
intervālā 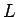 , pie tam
, pie tam
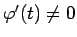 šajā intervālā; attēlo
intervālu
šajā intervālā; attēlo
intervālu 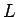 par kaut kādu intervālu
par kaut kādu intervālu 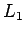 , kurā ir definēta
funkcija
, kurā ir definēta
funkcija 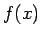 un
un 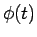 ir funkcijas
ir funkcijas
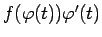 primitīvā funkcija intervālā
primitīvā funkcija intervālā 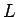 , tad
, tad
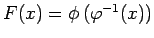 ir funkcijas
ir funkcijas 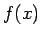 primitīvā
funkcija intervālā
primitīvā
funkcija intervālā 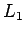 .
.
 Tā kā
Tā kā 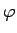 ir stingri monotona funkcija
intervālā
ir stingri monotona funkcija
intervālā 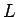 , tad tai eksistē apvērstā funkcija
, tad tai eksistē apvērstā funkcija
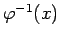 , kas ir definēta intervālā
, kas ir definēta intervālā 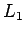 . Saskaņā ar
teorēmu par apvērstās funkcijas diferencēšanu funkcija
. Saskaņā ar
teorēmu par apvērstās funkcijas diferencēšanu funkcija
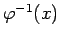 ir diferencējama, pie tam
ir diferencējama, pie tam
Atrod funkcijas
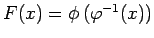 atvasinājumu,
diferencējot to kā saliktu funkciju.
atvasinājumu,
diferencējot to kā saliktu funkciju.
Seko, ka 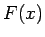 ir funkcijas
ir funkcijas 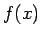 primitīvā funkcija.
primitīvā funkcija.
-
1.5. piezīme.
-

- No teorēmas seko, ka
Šī vienādība izsaka mainīgā aizvietošanas nenoteiktajā integrālī
būtību. Formulu lieto gan no kreisās puses uz labo pusi, t.i.,
mainīgo
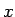 aizstājot ar kāda cita mainīgā
aizstājot ar kāda cita mainīgā 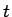 funkciju
funkciju
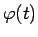 , gan otrādi, t.i., kādu funkciju apzīmējot ar jaunu
mainīgo.
, gan otrādi, t.i., kādu funkciju apzīmējot ar jaunu
mainīgo.
- Nedrīkst aizmirst pēc integrēšanas atgriezties pie
iepriekšējā integrēšanas mainīgā.
-
1.7. piemērs.
- Atrast
-
1.8. piemērs.
- Atrast
-
1.9. piemērs.
- Atrast
-
1.10. piemērs.
- Atrast
-
1.11. piemērs.
- Atrast
-
1.12. piemērs.
- Atrast
jo
-
1.6. piezīme.
- 1.7.-1.12. piemēros iegūtos integrāļus turpmāk izmanto kā
tabulāros. Šos integrāļus pievieno pamatintegrāļu
tabulai.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.5. Racionālu funkciju integrēšana
Augstāk: 1.4. Integrēšanas pamatmetodes
Iepriekšējais: 1.4.1. Parciālā integrēšana
2002-11-06
![]() Tā kā
Tā kā ![]() ir stingri monotona funkcija
intervālā
ir stingri monotona funkcija
intervālā ![]() , tad tai eksistē apvērstā funkcija
, tad tai eksistē apvērstā funkcija
![]() , kas ir definēta intervālā
, kas ir definēta intervālā ![]() . Saskaņā ar
teorēmu par apvērstās funkcijas diferencēšanu funkcija
. Saskaņā ar
teorēmu par apvērstās funkcijas diferencēšanu funkcija
![]() ir diferencējama, pie tam
ir diferencējama, pie tam
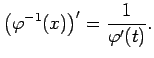
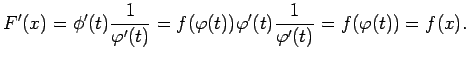
![]() ir funkcijas
ir funkcijas ![]() primitīvā funkcija.
primitīvā funkcija.
![]()